1. Алгебра
  2. Решить по теореме виета x2+2x-9=0

Решить по теореме виета x2+2x-9=0

Marattadjibov73 Marattadjibov73    2   06.04.2020 11:56    2

Ответы
АняЛари АняЛари  12.10.2020 17:09

x^2+2x-9=0\\\\x_1+x_2=-b\;\Rightarrow\; x_1+x_2=-2\\x_1\cdot x_2=c\;\Rightarrow\;x_1\cdot x_2=-9

И здесь начинается ступор. Дело в том, что корни этого квадратного уравнения будут не натуральными числами. Теорема Виета подходит только тогда, когда корни уравнения - целые числа. Попробую решить данное уравнение через Дискриминант.

x^{2} +2x - 9 = 0 \\\\ D = b^2-4ac=2^{2} - 4\cdot1\cdot(-9)= 4-(-36)=4+36=40

40 0 \; \Rightarrow 2 корня.

\sqrt{40}=\sqrt{4\cdot10}=2\sqrt{10}\\\\x_{1,2}=\dfrac{-b\underline+\sqrt{D}}{2a}\\\\x_1=\dfrac{-2+2\sqrt{10}}{2}= -1+\sqrt{10}\\\\x_2=\dfrac{-2-2\sqrt{10}}{2}=-1-\sqrt{10}

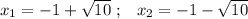
ответ: x_1= -1+\sqrt{10}\;;\;\;\;x_2=-1-\sqrt{10}

Как видим, такие ответы с Теоремы Виета представить невозможно.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
sashok0031 sashok0031  29.06.2019 22:00
Решите неравенство: 1) х в квадрате - 3 х - 4 меньше 0 2)3х в квадрате - 4х +8 больше или равно 0 3) -х в квадрате +3х -5 больше 0 4) х в квадрате +20х +100 меньше...
Reixerrr Reixerrr  29.06.2019 22:00
Какое из следующих утверждений верно: 1) диагонали ромба пересечения делится пополам. 2) в тупоугольном треугольнике все углы тупые. 3) каждая из биссектрис равнобедренного...
ladiaginairina ladiaginairina  29.06.2019 22:00
50 ! сложная текстовая ! из пункта a круговой трассы выехал велосипедист, а через 20 минут следом за ним отправился мотоциклист. через 5 минут после отправления он...
tisochkin123 tisochkin123  29.06.2019 22:00
Докажите что число 2375^2-2276^2 делится на 33 без остатка...
valya83 valya83  29.06.2019 22:00
Розвязать систему уравнений: {2х+у=9 {5х+2у=7...
ked00p08uz1 ked00p08uz1  29.06.2019 22:00
Один разделить на корень из двух плюс корень из восьми....
Yalikhan Yalikhan  29.06.2019 22:00
Найдите значение выражения: 24√2 cos⁡(-п/3) sin⁡(-п/4)...
Sashunai Sashunai  29.06.2019 22:00
Назовем углы 40,50,90,100 красивыми. сколько существует различных треугольников площади 1,все углы которых красивые...
trukit trukit  29.06.2019 22:01
50 ! 2 на движение 8.андрей ведет машину со скоростью 60 км/ч. он хочет проезжать каждый километр на полминуты быстрее. на сколько ему следует увеличить скорость?...
Aminka26 Aminka26  29.06.2019 22:01
Zв 8 степени умножить на z сколько будет?...

Популярные вопросы