1. Алгебра
  2. решить (очень полностью расписать,

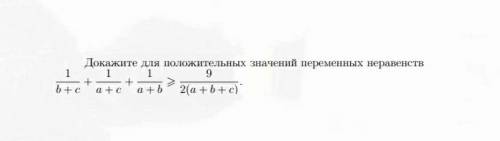
решить (очень полностью расписать, с объяснением)


решить (очень полностью расписать, с объяснением)

evelinkazelenyak evelinkazelenyak    1   11.07.2021 20:07    0

Ответы
kutluyulovarrr kutluyulovarrr  10.08.2021 21:14

Обозначим: b+c=x>0; a+c=y>0; a+b=z>0; неравенство превращается в

\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge \frac{9}{x+y+z}, что равносильно

(yz+xz+xy)(x+y+z)\ge 9xyz.

Чтобы доказать это неравенство, применим по отдельности неравенство Коши между средним арифметическим и средним геометрическим положительных чисел к обеим скобкам в левой части:

(yz+xz+xy)(x+y+z)\ge (3\sqrt[3]{yzxzxy})\cdot (3\sqrt[3]{xyz})=9\sqrt[3]{x^2y^2z^2}\cdot \sqrt[3]{xyz}=

=9\sqrt[3]{x^3y^3z^3}=9xyz

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kmvkemerovo kmvkemerovo  29.04.2021 19:35
10 2) Вырази в квадратных сантиметрах.50 м2 =4 м228 дм?6) Вырази в квадратных дециметрах:6 м2 =50 м2 =4800м2=в) Вырази в квадратных метрах:8 000 м2 =100 000 м2 =52 000 м2...
zaika787 zaika787  29.04.2021 19:37
Выполните действие:ах+ау/ху^2*х^2у/3х+3у 5/3а+7/4б...
nikita1247 nikita1247  29.04.2021 19:38
Розв яжіть неповні квадратні рівняння 4х²+1=0​...
LiliyaEgor LiliyaEgor  08.09.2019 04:20
Составьте уравнение, которое имеет корни а) 4 б) 4 и 2 в) 4; 2 и -3...
cbnybrjds cbnybrjds  08.09.2019 04:30
Решите 1.12x-(3x-5)+(9x-3), 2.4(x+0,2)=5x-3,8, решить 3.-4(5x-0,1)+18x+2, и найдите значение при x=-0,3 4. сравните значения выражений 0,4x-3 и -0,4x-3 при x=6...
marktopskiy34567 marktopskiy34567  08.09.2019 04:30
Вычислить интеграл от п до 0. 3x^2dx...
Cerega67 Cerega67  29.12.2020 10:04
Задача по алгебре про мяч​...
Леля24579 Леля24579  29.12.2020 10:05
Запишите в стандартном виде 1)4xy•x+xy²-10x²y2)4x⁶y³-x⁶x³+2x²y²-x²y...
AnToNoVa13 AnToNoVa13  29.12.2020 10:09
решить математику ( )3 функция неявная5 параметрическая...
crisisd crisisd  29.12.2020 10:09
Математика 2токсан тжб 5класс тауп берініздерші 5жұлдыз сразу​...

Популярные вопросы