Решить,, нужно найти точку минимума функции: f(x)=x^3/3-(a+1)/2*x^2+ax-7

Question

Алгебра: Решить,, нужно найти точку минимума функции: f(x)=x^3/3-(a+1)/2*x^2+ax-7

Sveto4ka2006 · Answer

кубическая функция может иметь только локальный минимум. Потому что при х ->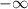 $-\infty$ она уходит в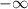 $-\infty$

точки минимума и максимума соответствуют нулям производной

( x^3/3-(a+1)/2*x^2+ax-7 )' = x^2 - (a+1)*x + a

сумма степеней равна нулю, значит один корень = 1, второй = a

локальным минимумом является больший корень (кубическая функция возрастает от минус бесконечности до первого корня, потом убывает, потом снова возрастает до плюс бесконечности)

значит при a<1 локальный минимум f(x=1) = 1/3 - (a+1)/2 + a - 7 = a/2 - 7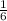 $\frac{1}{6}$