Решить, нужно. 1.найдите промежутки возрастания, убывания и точки экстремума функции y=2x^3-3x^2-36x+2. 2.найдите

Question

Алгебра: Решить, нужно. 1.найдите промежутки возрастания, убывания и точки экстремума функции y=2x^3-3x^2-36x+2. 2.найдите значение производной функции y=e^xумножитьsinx в точке x0=0. 3.является ли функция f(x)=x^4=x^2-3x=5 первообразной функции f(x)=4x^3=2x-3? . 1. в цилиндре высотой 10см. и площадью осевого сечения 40 см^2 площадь боковой поверхности, площадь полной поверхности и объём цилиндра. 2.найдите объём, площадь боковой поверхности тела, полученного при вращении прямоугольного треугольника с гипотенузой

tseng7788 · Answer

Дана функция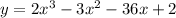 y=2x^3-3x^2-36x+2

Для нахождения экстемумов функции нужно сделать действия по следующиму алгоритму.

1. найти производную функции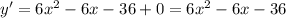 y'=6x^2-6x-36+0=6x^2-6x-36

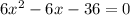
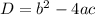
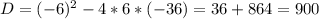
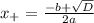
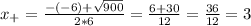
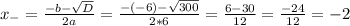
2. приравняем функцию к нулю и решим уравнение 6x^2-6x-36=0 D=b^2-4ac D=(-6)^2-4*6*(-36)=36+864=900 $x_+=\frac{-b+\sqrt{D}}{2a}$ $x_+=\frac{-(-6)+\sqrt{900}}{2*6}=\frac{6+30}{12}=\frac{36}{12}=3$ $x_-=\frac{-b-\sqrt{D}}{2a}=\frac{-(-6)-\sqrt{300}}{2*6}=\frac{6-30}{12}=\frac{-24}{12}=-2$