1. Алгебра
  2. Решить несколько показательных

Решить несколько показательных уравнений: 1)5^(x+1)+5^(x)+5^(x-1)=31 2)9*(1/4)^x -2*(1/2)^x=0 3)3^x-(1/3)^2-x=24

Nika1337228 Nika1337228    1   22.05.2019 04:20    63

Ответы
Розетта99 Розетта99  17.06.2020 05:42

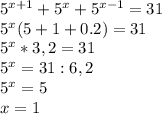
5^{x+1}+5^{x}+5^{x-1}=31\\\ 5^{x}(5+1+0.2)=31\\\ 5^{x}*3,2=31\\\ 5^{x}=31:6,2\\\ 5^{x}=5\\\ x=1

 

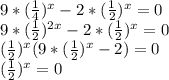9*(\frac{1}{4})^x -2*(\frac{1}{2})^x=0\\\ 9*(\frac{1}{2})^{2x} -2*(\frac{1}{2})^x=0\\\ (\frac{1}{2})^x(9*(\frac{1}{2})^x-2)=0\\\ (\frac{1}{2})^x=0   не удовлетворяет области определения показатльной фукнции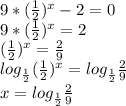  9*(\frac{1}{2})^x-2=0\\\ 9*(\frac{1}{2})^x=2\\\ (\frac{1}{2})^x=\frac{2}{9}\\\ log_\frac{1}{2}(\frac{1}{2})^x=log_\frac{1}{2}\frac{2}{9}\\\ x=log_\frac{1}{2}\frac{2}{9}

 

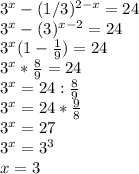
3^x-(1/3)^{2-x}=24\\\ 3^x-(3)^{x-2}=24\\\ 3^x(1-\frac{1}{9})=24\\\ 3^x*\frac{8}{9}=24\\\ 3^x=24:\frac{8}{9}\\\ 3^x=24*\frac{9}{8}\\\ 3^x=27\\\ 3^x=3^3\\\ x=3

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Hockeyist97 Hockeyist97  09.04.2020 10:29
Определите вид треугольника ABC, если его вершины имеют координаты:а) А(-2; -1), В(2; -1), C(-2; 1);б) А(-2; -2), B(2; -2), C(0; 1).​...
Dote8228 Dote8228  09.04.2020 10:29
1)В окружности проведены диаметры AB и CD.Докажите,что AB || CD.(Сделайте рисунок Из точки M, лежащей вне окружности,проведены к ней касательные MA и MB,где A и B-точки...
Mar09 Mar09  09.04.2020 10:29
Вычислите: ответ запишите в виде несократимой дроби....
NELly1237 NELly1237  09.04.2020 10:29
Найти площадь сектора колеса, соответствующую центральному углу 135 ° с радиусом 6 см. Радиусы 6 см-ге тең, 135°-қа тең центрлік бұрышқа сәйкес дөңгелектің секторының...
Dushanbe2003 Dushanbe2003  09.04.2020 10:29
Укажите наименьшее целое решение неравенства 5x+2 2(x-4)-3x...
20051207маша 20051207маша  09.04.2020 10:29
Какую часть площади круга составляет площадь сектора по центральному углу, равному 225 ° 225°-қа тең ценртлік бұрышқа сәйкес сектордың ауданы шеңбердің ауданының...
mikysya mikysya  04.03.2021 15:26
Дано: sin a = -0.4π меньше a меньше 3π\2Найти: cos 2a, tg a, ctg a...
Барбоси Барбоси  04.03.2021 15:27
Подайте у вигляді добутку: 16m²(x-12mnx ab+9n²x-9x-12ax-4a²x)​...
makhero111 makhero111  04.03.2021 15:27
Зная,что 2 x 7 и 8 y 28, оцените: а) x+y б)x-y в)xy г) x/y​...
TITANIKбро TITANIKбро  04.03.2021 15:28
3. используя формулы сокращение умножение вычисление . ) 101 202 91 + 81?48²+ 2 : 18*18 - 18² 48²-18²...

Популярные вопросы