, решить нерванство методом замены множителей.
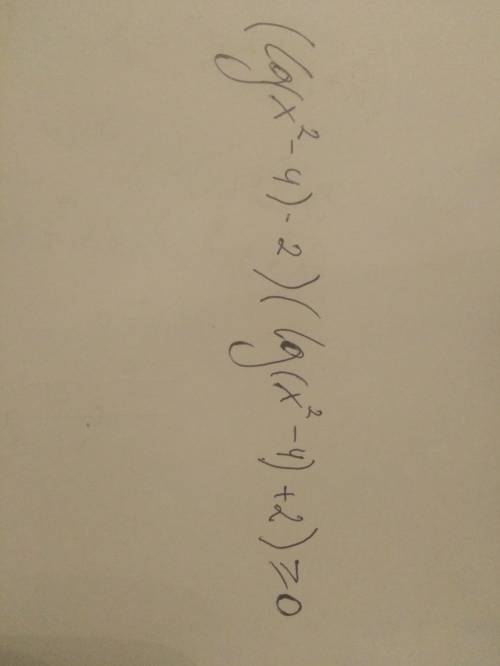
Другие вопросы по теме Алгебра
Популярные вопросы
- Вчем причины сходства природы северной части евразии и северной...
2 - Из города в деревню, расстояние между которыми равно 80 км, выехал...
2 - Как быстро подготовиться к диктанту? он завтра не знаю что делать,времени...
3 - Какие слова с двумя значениями может быть их много...
3 - Нужно найти точку максимума функции y=√29+2x -x^2...
3 - Соотнесите предложения и районы. 1 северный район. 2. центральная...
1 - Кроссворд ,на тему как человек открывал землю с вопросами и ответами...
3 - На рисунке ав=ад, вс=сд. докажите, что луч ас- биссектриса угла...
3 - Чтобы найти деитель, варианты ответа: произведение разделить на...
3 - Назовите ведущую тему повести «дубровский»: а) счастливая жизнь...
1
ответ:х∈(-∞;-2)∪(100;+∞)
Объяснение:
пусть lg(х²-4)=y; х²-4>0
___-22
+ - +
ОДЗ х∈(-∞-2)∪(2;+∞)
(y-2)(y+2)≥0
-22
+ - +
-∞≤у≤-2⇒lgх≤lg0.01
у≥2⇒lgх≥lg100
т.к. основание логарифма больше 1, то х≤lg0.01, с учетом ОДЗ
х∈(-∞;-2)∪(100;+∞)