Решить неравенство y'>0, если 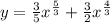
Другие вопросы по теме Алгебра
Популярные вопросы
- look , I can see books and paper Everyone Everywere...
3 - Ученый | СократПлатон| АристотельПифагорДемокритГиппократПлатон|...
2 - ЗАДАНИЕ: Прочитайте текст и напишите сочинение-рассуждение на...
1 - Выписать из художественной литературы 5 предложений обозначить...
3 - 3.Какие правила надо выполнять при работе в сети Интернет? смотреть...
2 - Don t worry he probably you later 1)will call 2)is goind to call 3)is...
3 - 1. Какой месяц короче всех? 2. Какая река самая страшная? 3. Может...
2 - .А.П. Чехова Хамелеон .Запиши действующих лиц рассказа. 2) Какие...
1 - ПООМГИТЕ УЖЕ НЕТ,ПЛ ГЛАВНЫЙ МОЗГ. ГЛАВНЫЙ МОЗГ. ГЛАВНЫЙ МОЗГ....
3 - Оставалось или что-то объединяющие русские земли...
3
+ - +
_____₀_____₀_____ m
- 2 0
/////////// ////////////
ответ : x ∈ (- ∞ ; - 8) ∪ (0 ; + ∞)