1. Алгебра
  2. Решить неравенство: [tex]

Решить неравенство: \sqrt{10 - x} ( {3}^{x - 7} - {4}^{x - 6} + 5) \leqslant 0​

KONERtm KONERtm    1   27.05.2019 13:22    0

Ответы
4РИМ 4РИМ  24.06.2020 15:56

Корень квадратный не может быть отрицательным. Значит, чтобы неравенство выполнялось, нужно, чтобы выражение в скобках было меньше, либо равно нуля.

\sqrt{10 - x}(3^{x-7} - 4^{x-6} + 5) \leqslant 0

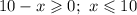
ОДЗ: 10 - x \geqslant 0; \ x \leqslant 10

3^{x-7} - 4^{x-6} + 5 \leqslant 0\\3^{x-7} \leqslant 4^{x-6} - 5

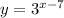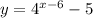Решим неравенство графически: построим график функции y = 3^{x-7} и y = 4^{x-6} - 5. Найдём те значения x, при котором вторая функция больше либо равна первой.

Пересечение графиков функций в точке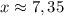 x \approx 7,35

Итак, функция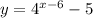 y = 4^{x-6} - 5 больше либо равна функции 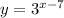y = 3^{x-7} на интервале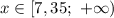 x \in [7,35; \ +\infty)

Объединим этот промежуток с ОДЗ и получим x \in [7,35; \ 10].

ответ: x \in [7,35; \ 10]


Решить неравенство: <img src=​" />
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
2003veronika07 2003veronika07  30.04.2020 08:43
Система уровнения подстановки 3x-10o=91 2x+o=-16 O это не ноль...
Юля0220 Юля0220  30.04.2020 08:41
Найдите значение выраженияa2 − 18 + 81 при не хочу двойку...
nicekuzia01 nicekuzia01  25.03.2021 18:06
Решите уравнение sin6x+√3cos 6x=-2cos8x​...
Engee Engee  25.03.2021 18:04
Знайти значення функції у=4-5х, якщо значення аргументу дорівнює -0,8...
Hah125 Hah125  25.03.2021 17:59
Задано функцію у= -3-8х. Знайти значення аргументу, якщо значення функції дорівнює -13...
easyanswer easyanswer  07.03.2020 02:34
Очень решить логарифмическое неравенство!...
kaukov03 kaukov03  07.03.2020 02:36
Сложите и вычтите алгебраические дроби....
Hemmgirl Hemmgirl  15.05.2020 13:23
Обчисліть значення виразу (x-x3) /2, якщо x=-корінь 5.​...
LeviAccem LeviAccem  15.05.2020 13:23
Чем материковая земная кора отличается от океанической ? выберите два верных ответа 1. материковая земная кора тоньше океанической 2. материковая земная кора толще...
danilpus2016 danilpus2016  15.05.2020 13:23
Хэлпуйте!! Буду блогадарен! За ранее...

Популярные вопросы