Решить неравенство методом интервалов: (x-2)(4-x)(x-3)^2> 0. решить неравенство методом интервалов: x+3/3-x меньше или равно 2 решить систему неравенств: {x^2-6x меньше или равно 0 {x-1< 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Какой механизм лежит в основе устройства весов? Рычаг Блок Наклонная...
1 - ) Определите, что выведет на экран программа при вызове...
2 - 4. Осуществить цепочку превращений. Br2-HBr-KBr-KCl-Cl2-HClO...
2 - Эссе на тему өз ой толғауым...
1 - можете написать про 4 сферы общества, любые подходящие новости из мира,...
2 - 3. Подберите видовую пару к глаголам (совершенный-несовершенный вид).Говорить,...
1 - 6 Second conditional. Write second conditional sentences using theprompts.1...
1 - За что ценят Казахстан на мировой арене?)...
1 - Технология экспресс приготовления блюд: 1) рассмотрите фотографии знакомы...
1 - расставьте припинания составьте схему отражающие постановку...
2
(x-2)(4-x)(x-3)^2>0
нули функции 2;3;4;
Т.к. (x-3)^2 выражение не может быть отрицательным, функция не доходит до нуля и возвращается не изменяя знак.
- + + -
___2____3___4_____
x ∈ (2;3) ∪ (3;4);
2) (x+3)/(3-x) ≤ 0;
на ноль делить нельзя x≠3;
нуль функции -3;
- + -
___-3____3___
x ∈ (-∞;-3] ∪ (3;∞);
3)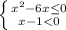
нули функции 6;0;
нули функции 1;
+ - +
____0_____6_______
[0;6]
- +
____1____
(-∞;1)
объединяем оба промежутка:
x ∈ [0;1)