Решить неравенство. Максимально подробно
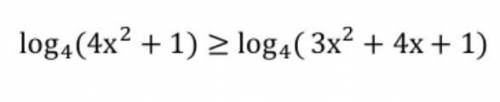
Другие вопросы по теме Алгебра
Популярные вопросы
- На высоте H = 200 км давление воздуха составляет примерно 10 −...
2 - В деревянный брусок, лежащий на гладкой горизонтальной поверхности,...
2 - Тележке массой m = 2,5 кг, стоящей на полу и соединённой со стеной...
1 - Начальная скорость снаряда, выпущенного из пушки вертикально вверх,...
1 - Два груза массами m1 = 2 кг и m2 = 4 кг, лежащие на гладкой горизонтальной...
3 - Какова разница в массе воздуха, при нормальном давлении заполняющего...
3 - В сосуд с водой бросают кусочка льда при непрерывном помешивании,...
1 - На горизонтальной поверхности лежит тело, на которое действует...
1 - Двум молям идеального газа при изобарном расширении сообщили ΔQ...
3 - Тело начинает двигаться из состояния покоя равноускоренно и за...
1
x ∈ (-∞, -1) ∪ (-1/3, 0] ∪ [4, +∞)
Объяснение:
находим ОДЗ x ∉ [ -1, -1/3 ] отсюда>>
область допустимых значений: x ∈ (-∞,-1) ∪ (-1/3, +∞)
Для а>1 выражение log a(x) ≥ log a(y) равно x≥y
4x^2 + 1 ≥ 3x^2 + 4x + 1
4x^2 ≥ 3x^2 + 4x
4x^2 - 3x^2 - 4x ≥ 0
x^2 - 4x ≥ 0
x ( x - 4 ) ≥ 0
возможны 2 случая когда произведение a*b будет ≥ 0.
(либо два отрицательных)
(либо два положительных)
Проверяем
x≥0 <=> x≥0 <=> x ∈ [4 , +∞ )
x-4≥0 x≥4
x ≤ 0 <=> x≤0 <=> x ∈ ( - ∞, 0 ]
x - 4 ≤0 x≤4
находим объединение для x ∈ ( - ∞, 0 ] и x ∈ [4 , +∞ ), получаем множество решений
МНОЖЕСТВО РЕШЕНИЙ x∈ (- ∞,0] ∪ [4, +∞) ,
ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ x ∈ (-∞,-1) ∪ (-1/3, +∞)
нахождение пересечения множеств решений и области допустимых значений
x ∈ (-∞, -1) ∪ (-1/3, 0] ∪ [4, +∞)
x ∈ (-∞, -1) ∪ (-1/3, 0] ∪ [4, +∞)
Объяснение:
находим ОДЗ x ∉ [ -1, -1/3 ] отсюда>>
область допустимых значений: x ∈ (-∞,-1) ∪ (-1/3, +∞)
Для а>1 выражение log a(x) ≥ log a(y) равно x≥y
4x^2 + 1 ≥ 3x^2 + 4x + 1
4x^2 ≥ 3x^2 + 4x
4x^2 - 3x^2 - 4x ≥ 0
x^2 - 4x ≥ 0
x ( x - 4 ) ≥ 0
возможны 2 случая когда произведение a*b будет ≥ 0.
(либо два отрицательных)
(либо два положительных)
Проверяем
x≥0 <=> x≥0 <=> x ∈ [4 , +∞ )
x-4≥0 x≥4
x ≤ 0 <=> x≤0 <=> x ∈ ( - ∞, 0 ]
x - 4 ≤0 x≤4
находим объединение для x ∈ ( - ∞, 0 ] и x ∈ [4 , +∞ ), получаем множество решений
МНОЖЕСТВО РЕШЕНИЙ x∈ (- ∞,0] ∪ [4, +∞) ,
ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ x ∈ (-∞,-1) ∪ (-1/3, +∞)
нахождение пересечения множеств решений и области допустимых значений
x ∈ (-∞, -1) ∪ (-1/3, 0] ∪ [4, +∞)