Решить неравенство и найти наименьшее натуральное число которое входит в его решение 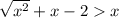
если что корень идёт на все выражение
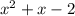
Другие вопросы по теме Алгебра
Популярные вопросы
- 50 просклоняйте по падежам слова: грустное мычание,бодрое рычание,дружеское...
3 - Заполните таблицу. бурые и красные водоросли. название среда особенности...
2 - Падежи у именах существительных в рассказе каждую осень деревья дарят...
3 - Ідоберіть 3 - 4 спільнокореневих слів до цих слів : будити, безлистяний....
3 - Які дива побачили гості на острові пушкін казка про царя султана...
3 - Кем был создан ливонский орден возглавлялся : а) великим князем;...
3 - Перевести на .зебра жывет в африке.любит кушать траву.она белая лошадь...
1 - Образец: 115ч.=4сут.19ч. 76ч.= 140ч.= 336ч.=...
2 - Потренируйся в правильном употреблении падежных форм числительных...
2 - Гусь весит 10кг, лебедь тяжелее на 8 кг., лиса легче лебедя на 6кг.,...
1
Объяснение:
см фото
а)х∈(-∞;-2]U(2;+∞)
б)3
Объяснение:
Рассмотрим 2 случая:
1) Если х<0,то
x²+x-2≥0
(х-1)(х+2)≥0
{ х≥1
{ х≤-2
Находим пересечение системы и нашего условия (х<0). Первой частью нашего ответа является х≤-2
P.S. выражение под корнем больше или равно нулю,так что сравнивать его с отрицательным числом нет смысла и мы выставляем условие ≥0
2) Если х≥0,то
х²+х-2>х²
х>2
Находим пересечение системы и нашего условия (х≥0). Второй частью нашего ответа является х>2
P.S. если корень больше положительного числа,то мы просто возводим в квадрат и знак выражения не меняется
Соединяя наши ответы получаем итог: х∈(-∞;-2]U(2;+∞)
ответ на второе задание: т.к. натуральными числами являются 1,2,3 и т.д.,то наименьшим будет 3,т.к. 2 не входит в решение неравенства