Решить неравенство f(x)>0, если f(x)=8x-x^2-x^3/3
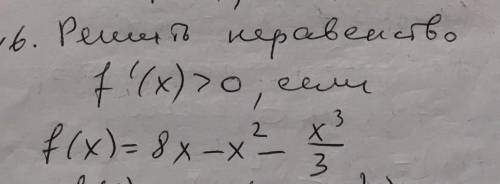
Другие вопросы по теме Алгебра
Популярные вопросы
- 1 I don t think my parents will let me go/ to go to therugby match on my own.2...
3 - без обмана! По горизонтали: 1. Какой музыкальный инструмент в переводе с французского...
3 - Найди значение буквенного выражения: а÷10+b×1000 при a = 123,2; b=0,0381....
3 - Война и мир РОЛЬ СЕМЬИ В РОМАНЕ, КАК ФОРМИРОВАЛИСЬ ЛИЧНОСТИ ГЕРОЕВ В СЕМЬЯХ?...
3 - Розгляньте фіксованих хрущів травневих . зверніть увагу на їхній колір і форму...
3 - Знайдіть яка маса солі і який об єм газу утворяться внаслідок реакції між 20...
1 - Шар епідермісу утворений живими клітинами які постійно діляться і забезпечують...
2 - She deleted the file from computer ( on / in / by ) mistake ....
3 - Задания по химии, 8 класс,...
3 - Здійсніть перетворення ацетилен бензен нітробензен анілін 2 4 6 триброманілін...
2
ашлащщақеешелщақақеқе
Дано: f(x) = 8x - x^2 - x^3/3
Шаг 1: Поставим неравенство, записав f(x) > 0
8x - x^2 - x^3/3 > 0
Шаг 2: Приведем неравенство к общему знаменателю, умножив обе части на 3:
3(8x - x^2 - x^3/3) > 0
24x - 3x^2 - x^3 > 0
Шаг 3: Приведем неравенство в вид полинома в убывающем порядке степеней:
-x^3 - 3x^2 + 24x > 0
Шаг 4: Факторизуем полином:
-x(x^2 + 3x - 24) > 0
Шаг 5: Разложим квадратный трехчлен на множители:
-x(x - 3)(x + 8) > 0
Шаг 6: Найдем значения x, которые удовлетворяют данному неравенству, применяя метод интервалов:
6.1: Найдем значения x, при которых полином равен 0. Это происходит, когда каждый из множителей равен 0:
x = 0, x - 3 = 0, x + 8 = 0
x = 0, x = 3, x = -8
6.2: Построим числовую ось и отметим точки, найденные в предыдущем шаге:
-8 0 3
6.3: Возьмем по одному интервалу между найденными значениями x и проверим знаки полинома внутри каждого интервала.
-8 < x < 0:
Подставим x = -9 в полином: -(-9)(-9 - 3)(-9 + 8) = -9(12)(-1) = 108 > 0
Полином положительный на этом интервале.
0 < x < 3:
Подставим x = 1 в полином: -(1)(1 - 3)(1 + 8) = -(1)(-2)(9) = 18 > 0
Полином положительный на этом интервале.
x > 3:
Подставим x = 4 в полином: -(4)(4 - 3)(4 + 8) = -(4)(1)(12) = -48 < 0
Полином отрицательный на этом интервале.
Шаг 7: Объединим интервалы, на которых полином положительный:
Итак, неравенство f(x) > 0 выполняется для всех x из интервала (-8, 0) и (0, 3].
Таким образом, решением данного неравенства является интервал (-8, 0) объединенный с интервалом (0, 3].