Решить неравенство
cos9x+4cos3x> 0

Объяснение:

Используем  формулу косинуса тройного угла и выносим затем общий множитель за скобки:

Замечаем, что второй множитель всегда положителен, поскольку имеет вид суммы квадрата, который всегда неотрицателен, и единицы, прибавление которой делает все выражение только положительным. Первый же множитель уже может быть как положительным, так и отрицательным. Стало быть, для положительности всего произведения он должен быть только положительным. Значит, неравенство равносильно следующему:

Это неравенство уже вполне известно, как решать. Сначала ради удобства сделаем замену .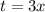

Ну и дальше это простейшее неравенство решаем с окружности.

Относительно t решение:

Относительно x: