Решить неравенство без графика

Равенство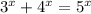 возможно только при х = 2 (т. Пифагора). Отсюда следует, что  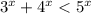 при х > 2.

ответ: x ≥ 2.

тк  5^x  положительно при любом  x ,  то  можно  поделить обе часть  на:

5^x  не  боясь за перемену знака неравенства:

(3/5)^x   +(4/5)^x- 1<=0

Cумма   степенных функций монотонная функция ,(тк  сумма монотонных функций функция монотонная),  а  значит пересекает ось  x  в одной точке.  Подбором сразу видно что  x=2.   При  увеличении x значение функции   убывает,  тк  3/5<1  и 4/5<1 ,  таким образом решение: x>=2

ответ: x>=2