Алгебра: Решить не графическим методом

Решить не графическим методом

Ответы

NHatynceva 12.07.2022 14:40

ответ: 5

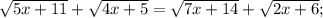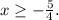
Объяснение: $\sqrt{5x+11}+\sqrt{4x+5}=\sqrt{7x+14}+\sqrt{2x+6};$ ОДЗ: $x\ge -\frac{5}{4}.$

Корень x=5 угадываем (6+5=7+4 - верно). Замена: x+2=p; x=p-2;

$\sqrt{5p+1}+\sqrt{4p-3}=\sqrt{7p}+\sqrt{2p+2};$ $p\ge \frac{3}{4}.$ Делим уравнение на $\sqrt{p}$ и обозначаем $\frac{1}{p}$ буквой q; $q\in (0;\frac{4}{3}]$ . Получается уравнение

$\sqrt{5+q}+\sqrt{4-3q}=\sqrt{7}+\sqrt{2+2q}.$ Угаданный корень x=5 для исходного уравнения приводит к корню q=1/7 полученного уравнения (подстановка подтверждает это). Докажем, что других корней нет. Для этого с производной убедимся, что левая часть убывает, а правая возрастает. С правой частью всё понятно, разберёмся с левой: $f(q)=\sqrt{5+q}+\sqrt{4-3q};\ f'(q)=\frac{1}{2\sqrt{5+q}}-\frac{3}{2\sqrt{4-3q}};$

эта производная равна нулю при 4-3q=9(5+q); 12q=-41; q=-41/12∉(0;4/3]. Поэтому на интервале (0;4/3) производная не меняет знак. Легко убедиться, что этот знак отрицательный, устремив, например, q к 0. Поэтому функция f(q) убывает, а раз функция в правой части уравнения возрастает, другого решения кроме q=1/7 быть не может.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра