1. Алгебра
  2. Решить. найти частное решение

Решить.
найти частное решение дифференциального уравнения

danilkudo423 danilkudo423    2   18.10.2019 10:16    0

Ответы
pelmen123456789 pelmen123456789  10.10.2020 07:44

Найти частное решение дифференциального уравнения:

y''+3y'+2y=0, y(0)=2, y'(0)=1

Данное дифференциальное уравнение является однородным. Перейдем к характеристическому уравнению, выполнив замену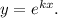 y=e^{kx}.

k^2+3k+2=0\\

k_1=-2\\ k_2=-1

Общее решение дифференциального уравнения:

y=C_1e^{-2x}+C_2e^{-x}

Найдем теперь частное решение нашего диф. уравнения

y'=-2C_1e^{-2x}-C_2e^{-x}

Подставим начальные условия

\displaystyle \left \{ {{2=C_1+C_2} \atop {1=-2C_1-C_2}} \right.

Сложив обе уравнения, получим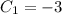 C_1=-3, тогда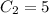 C_2=5

Частное решение: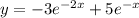 y=-3e^{-2x}+5e^{-x}

ПОКАЗАТЬ ОТВЕТЫ
Ріo78 Ріo78  10.10.2020 07:44

ответ: во вложении Объяснение:


Решить. найти частное решение дифференциального уравнения
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Ermolenkoo Ermolenkoo  10.06.2019 17:20
Решите уравнение 1,2(5-4х)=-6(0,8х+1)...
ванюшаплай ванюшаплай  10.06.2019 17:20
1. сложите верные числовые равенства а) 6,7 -4,7 и -15,4 -18,3 б) -5,3 5,8 и 4 -3,3 3. б) х(в кубе) - х(в квадрате) - 25х + 25 в) 36b(в квадрате) - (6-b)(в квадрате)...
AlsiMaksimowa AlsiMaksimowa  10.06.2019 17:20
Представьте разными в 8 степени в виде произведения: а) двух степеней с основанием 3 б) трех степеней с основанием 3 в) четырех степеней с основанием 3. ! : *(...
Sfdfgc Sfdfgc  10.06.2019 17:20
Решить уравнение : а). 5у + 27=4у + 21....
katerinaplachet katerinaplachet  10.06.2019 17:20
Цену товара три раза снижали на 20%. на сколько процентов изменилась стоимость товара по сравнению с первоначальной?...
Chevalier26 Chevalier26  19.08.2019 02:10
Постройте на листе график функции : y=-2x...
syrok20031812 syrok20031812  19.08.2019 02:10
Как решить пример 16ч21мин-8ч45мин и обьясните...
позитив19 позитив19  19.08.2019 02:10
Верно ли тождество? (2а+√b)² = 4a²+2a√b+b...
elmira64 elmira64  24.10.2020 08:30
Решите уровнения 49-(- y )=-13 А) 36 б) -62 в) 0 г) 62...
Лапулька123 Лапулька123  24.10.2020 08:30
Уравнение 2,8-x=7(0,2+0,5) m-1,2(2-m)=1+2m 8y-9-(4y-5)=1,2y-(4-5y)...

Популярные вопросы