решить на фото с полным решением

1)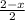 + 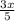= 4 I ·2·5

5·(2-x) + 2·3x = 4·2·5

10-5x+6x=40

-5x+6x=40-10

x=30

2)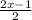 + 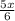- 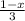= 3x-2 I·6

3·(2x-1) + 5x - 2·(1-x) = 6·(3x-2)

6x-3+5x-2+2x=18x-12

6x+5x+2x-18X=3+2-12

-5x=-6

x=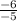

x= 1,2

3)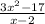 =2x+4

Область допустимых значений: x-2≠0, x≠2

Значит можем домножить все выражение на x-2≠0, тогда

3x² - 17=(x - 2)·(2x + 4)

3x² - 17=2x²- 4x + 4x - 8

3x²-17-2x²+4x-4x+8=0

x²-11=0

x²=11

x=±√11

4)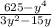 = 0

Область допустимых значений: 3y²-15y≠0

                                                        3y(y-5)≠0

                                                         3y≠0       y-5≠0

                                                          y≠0        y≠5

Чтобы дробь была равна нулю, числитель должен быть равен нулю ⇒

625-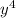=0

=625

y=5      или       y=-5

y=5∉ОДЗ        

y= - 5

Это все, с чем я могу