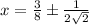решить логарифмическое уравнение (номер 817)
P.S решение с другого примера (так нужно;))
Другие вопросы по теме Алгебра
Популярные вопросы
- Светом какой частоты надо получить калий чтобы кинетическая энергия вырванного...
2 - Хворий 25 років після вживання грибів через 12 годин відчув ознаки нездужання....
3 - Выпишите из текста 2 предложения, содержащие сказуемое в пассивном залоге....
1 - Осуществить превращение CaC2→C2H2→C2H4→C2H5OH→CH3COH→CH3COOH...
1 - Выпишите из текста предложения, содержащие сказуемое в активном залоге....
2 - Валерий поместил в банк вклад в размере 40 млн рублей на четыре года...
1 - с химией. Задание 1. Составьте структурные формулы двух гомологов и двух...
2 - кроме номера кроме номера 3 >...
3 - с математикой с математикой >...
1 - 5. Choose the correct variant. girl over there who is singing a nice...
2
Теперь выпишем все ограничения на x:
Очевидно, что оба корня подходят.
ответ: