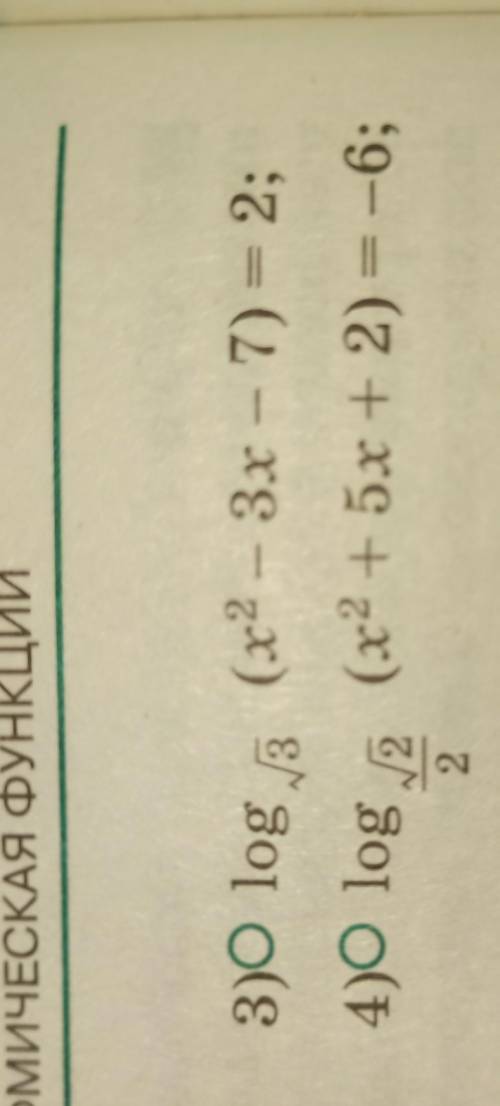
Решить логарифмическое уравнение 3.4
с объяснением
Другие вопросы по теме Алгебра
Популярные вопросы
- Страна, в которую ездил Гайдн после того, как ему исполнилось 60 лет? Россия,Франция,...
3 - Найти x, с деления 4Ро*Vo=3To*RY на каждое выражение: 1) xPo*2Vo=2To*RY 2)xPo*3Vo=3To*RY...
1 - Тест по ОБЖ 9 класс терроризм 1.Терроризм – это идеология _ и практика на принятие...
2 - 121. Ynotpente raronul B Past Simple. ($ 16, § 19)1. He drinks milk.He He2. He...
2 - Нужно написать сочинение на тему : Русская земля славятся талантами ...
3 - 0,5:3=1 1/3:xРешите уравнение...
3 - Можно ли современные демократические страны сравнить с Афинами времен Солона...
1 - РАБОТА В ПАРЕ 5Вычисли с проверкой.256 500 : 27106 110 : 786256 626 : 80713 888...
1 - Отзывы музики барокко нужно написать композитора песню и отзыв...
1 - При пилении пила застряла в древесине. Что нужно делать, чтобы пила не застревала...
2
3)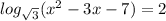
ОДЗ: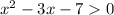 =>
=> 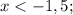
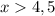
ответ: {-2; 5}
4)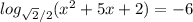
ответ: {-6; 1}