1. Алгебра
  2. Решить логарифмические

Решить логарифмические уравнения: lg(x+√3)+lg(x-√3)=0; log₂(x-2)+log₂(x-3)=1; lg(x²-9)-lg(x-3)=0; log₆(x-1)-log₆(2x-11)=log₆2; log₀,₇log₄(x-5)=0; log²₀,₅x-log₀,₅x-2=0;

Nanaw45 Nanaw45    2   22.05.2019 06:30    22

Ответы
xtreil181пингвинчик xtreil181пингвинчик  17.06.2020 09:25

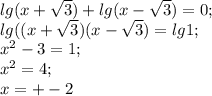
lg(x+ \sqrt{3})+lg(x-\sqrt{3})=0;\\ lg((x+ \sqrt{3})(x-\sqrt{3})=lg1;\\ x^{2}-3=1;\\ x^{2}=4;\\ x=+-2

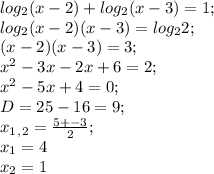
log_2(x-2)+log_2(x-3)=1;\\ log_2(x-2)(x-3)=log_22;\\ (x-2)(x-3)=3;\\ x^{2}-3x-2x+6=2;\\ x^{2}-5x+4=0;\\ D=25-16=9;\\ x_1_,_2=\frac{5+-3}{2};\\ x_1=4\\ x_2=1

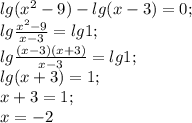lg(x^{2}-9)-lg(x-3)=0;\\ lg\frac{x^{2}-9}{x-3}=lg1;\\ lg\frac{(x-3)(x+3)}{x-3}=lg1;\\ lg(x+3)=1;\\x+3=1;\\ x=-2 нет решений

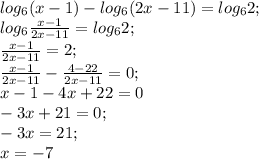log_6(x-1)-log_6(2x-11)=log_62;\\ log_6\frac{x-1}{2x-11}=log_62;\\ \frac{x-1}{2x-11}=2;\\ \frac{x-1}{2x-11} - \frac{4-22}{2x-11}=0;\\ x-1-4x+22=0\\ -3x+21=0;\\ -3x=21;\\ x=-7 ytn htitybq

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
NikaAs1 NikaAs1  12.12.2021 18:23
Там где где я написала 6соs^2 (это значит во второй степени) А то что в скобках, снизу должно быть это под ( п-2х) должно быть ( 2 )Решите уравнение:6cos2(п-х)-5cos(п-2х)...
duminalarisa duminalarisa  12.12.2021 18:24
Освободитесь от иррациональности в знаменателе дроби: a) 1/2 корень из 5б) 8/корень из 7 - 1...
zverrodion199911 zverrodion199911  12.12.2021 18:24
Решение не обязательно, просто ответ....
nekit1205 nekit1205  10.07.2019 10:00
Постройте график функции у=-х^2+2х+8...
AlanaBelkina AlanaBelkina  10.07.2019 10:00
Сколько будет: 2х-х во второй степени. х во второй степени - 10 х....
zamanova05 zamanova05  10.07.2019 10:00
Як побудувати график квадратичнои функции у=3х^2-10х...
Elenamikki Elenamikki  10.07.2019 10:00
Разложите на множители 12а2у2-6аус+3ас2-6а2ус-с+2ау...
danila2001k danila2001k  10.07.2019 10:00
2в 30 степени : 8 в 9 степени =? сколько будет? и как решать?...
chuckcher chuckcher  10.07.2019 10:00
Какое число должно стоять в пустой ячейке? 58,37,28,49,?...
vadimgofman vadimgofman  10.07.2019 10:00
Решительно : √3/3-√3 корень из 3 делённый на 3 - корень из 3....

Популярные вопросы