1. Алгебра
  2. Решить линейное уравнение методом

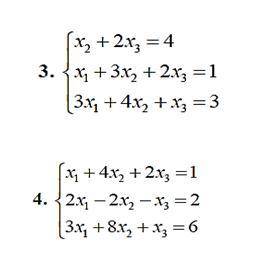
Решить линейное уравнение методом крамера


Решить линейное уравнение методом крамера

bbigigitovadakit bbigigitovadakit    2   18.11.2020 13:43    3

Ответы
Семрал Семрал  18.12.2020 13:52

Объяснение:

3.

Запишем эту систему в матричной форме: Ах=b.

A=\left(\begin{array}{ccc}0\ 1\ 2\\1\ 3\ 2\\3\ 4\ 1\end{array}\right) \ \ \ \ b=\left(\begin{array}{ccc}4\\1\\3\end{array}\right).\\

Найдём определитель матрицы Δ:

\Delta=0*(3*1-2*4)-1*(1*1-2*3)+2*(1*4-3*3)=\\=0*(3-8)-(1-6)+2*(4-9)=0*(-5)-(-5)+2*(-5)=5-10=-5.

Заменим 1-й столбец матрицы A на вектор столбца b:

A_1=\left(\begin{array}{ccc}4\ 1\ 2\\1\ 3\ 2\\3\ 4\ 1\end{array}\right)\\

\Delta_1=4*(3*1-2*4)-1*(1*1-2*3)+2*(1*4-3*3)=\\=4*(3-8)-(1-6)+2*(4-9)=4*(-5)-(-5)+2*(-5)=-20+5-10=-25.

Заменим 2-й столбец матрицы A на вектор столбца b:

A_2=\left(\begin{array}{ccc}0\ 4\ 2\\1\ 1\ 2\\3\ 3\ 1\end{array}\right) .

\Delta_2=0*(1*1-2*3)-4*(1*1-2*3)+2*(1*3-1*3)=\\=0*(1-6)-4*(1-6)+2*(3-3)=0*(-5)-4*(-5)+2*0=20.

Заменим 3-й столбец матрицы A на вектор столбца b:

A_3=\left(\begin{array}{ccc}0\ 1\ 4\\1\ 3\ 1\\3\ 4\ 3\end{array}\right) .

\Delta_3=0*(1*4-3*3)-1*(1*3-1*3)+4*(1*4-3*3)=\\=0*(4-9)-1*(3-3)+4*(4-9)=0*(-5)-1*0+4*(-5)=-20.

x_1=\frac{\Delta_1}{\Delta} =\frac{-25}{-5} =5.\\x_2=\frac{\Delta_2}{\Delta}=\frac{20}{-5} =-4.\\x_3=\frac{\Delta_3}{\Delta}=\frac{-20}{-5} =4.

ответ: x₁=5, x₂=-4, x₃=4.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Fetissh1 Fetissh1  30.06.2019 04:50
1).х^4-9х^2=0 2). (х+18)/4-(4х-3)/3=7...
TKluykova TKluykova  30.06.2019 04:50
Моторная лодка км против течения реки и 8 км по течению,потратив на весь путь 1 час.какая скорость лодки в стоячей воде,если скорость течения реки равно 2 км\ч?...
федя172 федя172  30.06.2019 04:50
(5ас^2/a^2-4c^2)*(a-2c/ac) при a=-5.2; c=-2.4 найти значение выражения...
snezhanavasileozvjsv snezhanavasileozvjsv  30.06.2019 04:50
^(2 степень) разложите на множители. а)3x^-30x+75 б)3a^-3b^-a+b...
Гилязарт Гилязарт  30.06.2019 04:50
Найдите значение выражения 36sin23cos23/sin46...
ira231006 ira231006  30.06.2019 04:50
Укажите область определения функции и постройте ее график. надо...
fox363 fox363  30.06.2019 04:50
Найдите значение производной функции y=2x\4x+3 в точке x0=1\4...
MadPrinter MadPrinter  30.06.2019 04:50
Объясните как решается, нужно. 1)0.07*(-10)^3+5*(-10)^2+3 2)(3*10^-2)^2*(12*10^4) 3)3*10^-2+4*10^-3+9*10^-4 4) 6-х = 2х х-1...
viktorey viktorey  30.06.2019 04:50
Забыла как расписывать, , , т.е не ответ, а расписать....
tv240067 tv240067  11.09.2019 13:50
Найти положительный корень уравнения: 1) (х-2)×(х+3)=0 2) (х-7)×(х+7)=0 можно с решением! )...

Популярные вопросы