Решить квадратные уравнения: а) 2x2 + 5x – 3 = 0

б) 2x2 – 9x = 0

в) x2 – 14x + 40 = 0 (через теорему Виетта)

a) 2x^2 + 5x - 3 = 0

Через дискриминант:

D = 25 + 4 * 3 * 2 = 49

= (-5 ± √49)/4

x1 = 1/2

x2 = -3

б) 2x^2 - 9x = 0

Выносим х:

x(2x-9) = 0

x1 = 0

x2 = 9/2

в) x^2 - 14x + 40 = 0

По т. Виета:

x1 + x2 = 14

x1 * x2 = 40

Подобрать легко:

x1 = 10

x2 = 4

Объяснение:

Смотри решение.

Объяснение:

1) Решаем 1 уравнение:

2) Решаем 2 уравнение:

ответ: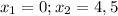

3) Решаем 3 уравнение:

По теореме Виета:

Сумма корней уравнения равна второму члену  уравнения (b) с противоположным знаком:

Произведение корней уравнения равно свободному члену уравнения:

На основании выше изложенной теории получаем решение:

Откуда получаем корни уравнения: