1. Алгебра
  2. Решить , кому показала никто не

Решить , кому показала никто не смог =( определите tgx из уравнения : 5sin(x+п/3 ) = 7sin(п/6 - х )

DogyStyleee DogyStyleee    3   25.05.2019 08:00    0

Ответы
angelok8408 angelok8408  01.10.2020 11:22
Надо раскрыть формулы синус суммы и синус разности.Получим
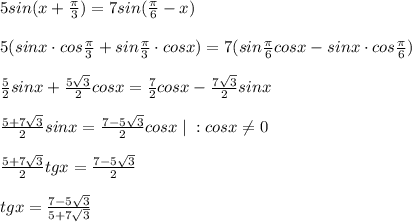
 5sin(x+\frac{\pi}{3})=7sin(\frac{\pi}{6}-x)\\\\5(sinx\cdot cos\frac{\pi}{3}+sin\frac{\pi}{3}\cdot cosx)=7(sin\frac{\pi}{6}cosx-sinx\cdot cos\frac{\pi}{6})\\\\\frac{5}{2}sinx+\frac{5\sqrt3}{2}cosx=\frac{7}{2}cosx-\frac{7\sqrt3}{2}sinx\\\\\frac{5+7\sqrt3}{2}sinx=\frac{7-5\sqrt3}{2}cosx\; |\; :cosx\ne 0\\\\\frac{5+7\sqrt3}{2}tgx=\frac{7-5\sqrt3}{2}\\\\tgx=\frac{7-5\sqrt3}{5+7\sqrt3}
ПОКАЗАТЬ ОТВЕТЫ
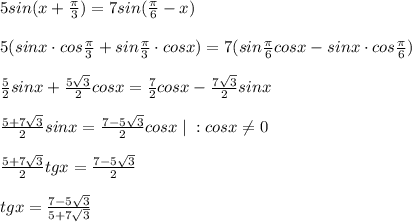
Другие вопросы по теме Алгебра
omon3565 omon3565  23.04.2020 21:46
Прямая y=kx+b проходит через точки a (-3;-1) и b (2;5) найдите k и b и запишите уравнение этой прямой​...
EllenOnyschuk EllenOnyschuk  23.04.2020 21:46
Решите уравнение :2x^2-8x/3=0...
311020029332 311020029332  20.09.2019 13:00
Сдвух яблонь собрали 67 кг яблок,причем с одной яблони собрали на 19 кг больше,чем с другой.сколько килограммов яблок собрали с каждой яблони?...
prynik99 prynik99  20.09.2019 13:00
Вынесение общего множетеля за скобки 8а²+3а-2а³...
elenak22 elenak22  20.09.2019 13:00
A)y=x³+2x²-5x+3 при x=-1; б)y=7t+2 при t=2 14t-3 7 решите...
СавелийРямов СавелийРямов  27.07.2019 18:00
Найдите 21 член в арифметической прогрессии, если а4=17, d=4....
NiceSaid NiceSaid  27.07.2019 18:00
1. 8 стрелков ведут огонь по 6 целям и каждый выбирает цель произвольно. какова вероятность, что все стрелки стреляют по разным целям?...
tiger071 tiger071  27.07.2019 18:00
Вычислить: a)27/32 · 8/162 · 72/69 b)38/147 · 91/152 : 65/264...
hmelova hmelova  27.07.2019 18:10
Одна из сторон прямоугольника га 5 см больше другой. найдите стороны прямоугольника, если его площадь равна 14см2...
evasaidova91 evasaidova91  27.07.2019 18:10
Разложи на множители x^3+8x^2−4x−32...

Популярные вопросы