Решить иррациональные уравнения
нужно
Другие вопросы по теме Алгебра
Популярные вопросы
- Морфологический разбор слова у ручья...
1 - Ребусты шеш.шешуіндегі сөзге әңгіме құра.концерт....
2 - (к предмету, это не относится) подскажите , как могут расшифровывается...
1 - Найдите значение выражение (49xy-0,+7/8y) при x=-1 3/7, y=-1 1/7...
2 - Перевести сказку goldilocks and the three bears baby who is this?...
2 - Тур ходит по горам, турица по долгам, тур свистнет, турица мигнёт-отгадайте...
1 - Найди границы в которых заключены произведениями 176 умножить на...
3 - Мама називає олю помічницею, бо донька їй в усьому є. оля продовжити...
3 - Описать индюка в художественно стиле...
1 - Решить уравнение: 3 х (1+2х) + 8 = 32...
3
Из-за ограничения будет только 1 корень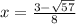
Ограничение и только один будет корень x=-2
x=-3 из-за ограничения