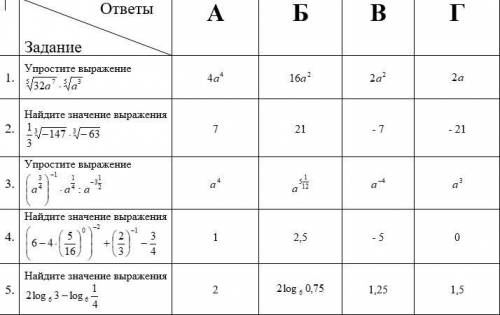
решить хотя бы 6-5 заданий. Желательно с подробным решением

Другие вопросы по теме Алгебра
Популярные вопросы
- Какая протестантская церковь запрещала праздники, развлечения, музыку, нарядную...
1 - Дайте характеристику географического положения Казахстана по плану. Положение...
1 - 3 Choose the correct words.1 Look where you re running, or you ll sprain / cut...
2 - Что увидел и почувствовал Саня в таёжном лесу? На основании этих наблюдений сделайте...
2 - Текст задания: 1. Свойства пределов функции в точке. Замечательные пределы. 2.Установите...
2 - Нужно соотнести страну к во В каких их этих стран изменения мирным путём?? 2Не...
3 - Які повітряні маси формують клімат Північної Амерки? Які вітри їх переміщують?...
1 - Зробіть фізику (скільки зможете номера будь ласка:)...
1 - Причины екологичнои кризи Шляхи подолання екологичнои кризы...
2 - Представьте в виде блок-схемы следующую народную примету: Если белка строит гнездо...
1
1)
ответ: В.
2)
ответ: А.
3)
ответ: Г.
4)
ответ: А.
5)
ответ: А.
6)
Для начала решим систему неравенств, определяющую область допустимых значений :
:
Возводим обе части уравнения в квадрат.
По теореме Виета:
3 не подходит под область допустимых значений.
ответ: корень только один, и он положительный.
7)
ответ:![(-9; -7]](/tpl/images/1579/1990/86283.png) .
.
8)
Областью определения функции является решение следующего неравенства:
Так как основание меньше единицы, то:
ответ:![(-\infty; 1,5]](/tpl/images/1579/1990/b9ec0.png) .
.
9)
Найдём область значения функции.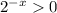 , тогда
, тогда 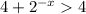 . Значит,
. Значит, 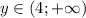 . Следовательно, из перечисленных чисел в множество значений входит только 5 (4 не входит, так как концы не включаем).
. Следовательно, из перечисленных чисел в множество значений входит только 5 (4 не входит, так как концы не включаем).
ответ: 5.
10)
Условие чётности функции: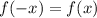 . Проверяем для каждой.
. Проверяем для каждой.
ответ: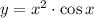 .
.