Решить графически уравнение: 8x^-3 = (x+1)^3 можете хотя бы просто объяснить, как строить 8x^-3 ?

Чтобы решить графически уравнение, нужно построить два графика:  для функции слева и функции справа от знака равенства.

1)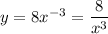    -  степенная функция с отрицательным показателем (-3) называется гиперболой третьего порядка. Ветви параболы расположены в первой и третьей четвертях  (k=8 > 0)

Область определения  x≠0   ⇒   x ∈ (-∞; 0) ∪ (0; +∞)

Область значений функции   y ∈ (-∞; 0) ∪ (0; +∞)

Точки для построения  

x :   1      -1       2     -2       4       -4

y :   8     -8      1       -1       1/8     -1/8

2)   y = (x + 1)³    -   степенная функция с натуральным показателем.  График - кубическая парабола.

Область определения  x ∈ R

Область значений функции   y ∈ R

Точки для построения  

x :   0       1      -1       2      -2      -3

y :   1        8      0      27     -1       -8

Графики представлены в приложении.

Графики пересекаются в двух точках  А(1; 8)  и  B(-2; -1).  Координаты  х точек пересечения являются решением уравнения   .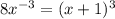

ответ :  x₁ = 1;  x₂ = -2