, решить : если |z| = 1 , то z-1/z+1 является мнимым числом!?
Другие вопросы по теме Алгебра
Популярные вопросы
- Қазақ тілі секірді тасыды сөзіне сөйлем керек...
3 - Начертите прямую перепендикулярную прямой а помгите только чтоб...
3 - Решите подробно,(х+2)=2х-4 заранее ❣...
3 - Докажите тождество: 1.(y+9)(10-3y+y^2)-0,5y(12y-34)=90+y^32. (2a^2-a+11)(8a-3)+7a(-13+2a)=-33+16a^33....
1 - Придумать рассказ на какую-нибудь пословицу...
1 - Начертите какую нибудь прямую перпендикулярную прямой а...
1 - Перевести на казахский язык.. 1.я люблю малиновое морожено.2.я...
1 - Куліш пантелеймон — орися тема идея 100...
1 - Форма правления в россии до 1905 года представляла собой...
1 - Капните пенициллин на плесень. что произойдёт? как скоро будут...
3
Да,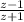 является чисто мнимым числом.
является чисто мнимым числом.
Объяснение:
Рассмотрим выражение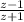 :
:
Представим его в алгебраической форме: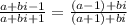 .
.
Домножим числитель и знаменатель дроби на комплексно сопряжённое знаменателю:
Знаменатель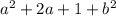 уже действительный.
уже действительный.
Рассмотрим числитель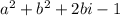 :
:
Число будет чисто мнимым, если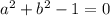 , то есть
, то есть 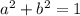 . А как известно, модуль исходного комплексного числа равен единице, то есть условие соблюдается. Таким образом,
. А как известно, модуль исходного комплексного числа равен единице, то есть условие соблюдается. Таким образом, 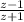 является чисто мнимым числом.
является чисто мнимым числом.