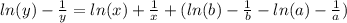Решить дифференциальные уравнения с разделяющими переменными и коши

Ответы

Kam09 24.05.2020 15:17

Разделим все на dx получим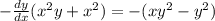 $-\frac{dy}{dx}(x^2y+x^2)=-(xy^2-y^2)$

Сделаем так чтобы в левой части осталось только dy/dx

Получим

$\frac{dy}{dx}=\frac{xy^2-y^2}{x^2y+x^2}=\frac{y^2}{y+1}\frac{x-1}{x^2}$

Теперь умножим все на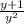 $\frac{y+1}{y^2}$ получаем:

$\frac{y+1}{y^2}dy=\frac{x-1}{x^2}dx$

Возьмем интеграл от левой и правой части

$\int{\frac{y+1}{y^2}}dy=\int{\frac{x-1}{x^2}}dx$

Находим значения интегралов получаем:

$ln(y)-\frac{1}{y}+C=ln(x)+\frac{1}{x}+C^1$ Можно объеденить С и С1 в одну константу, назовем ее С.

Этого я думаю достаточно. Чтобы решить задачу Коши нужны начальные условия, к сожалению здесь они не предоставлены. Поэтому попытаемся решить задачу Коши для произвольных начальных условий

y(a)=b , где a,b-константы

найдем сразу ln(y(a))=ln(b) и подставим все в уравнение

получим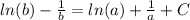 $ln(b)-\frac{1}{b}=ln(a)+\frac{1}{a}+C$

Отсюда

$C=ln(b)-\frac{1}{b}-ln(a)-\frac{1}{a}$

Т.е решеним задачи Коши для произвольных a и b, которые конечно должны принадлежать области определения функций указанных в общем решении уравнения (очевидно, что а и b не равны 0, т.к деление на ноль недопустимо и в общем то говоря а и b>0, если мы конечно не рассматриваем случая когда логарифмическая функция продолжается на комплексное пространство) будет: $ln(y)-\frac{1}{y}=ln(x)+\frac{1}{x}+(ln(b)-\frac{1}{b}-ln(a)-\frac{1}{a})$