1. Алгебра
  2. Решить дифференциальное уравнение:y

Решить дифференциальное уравнение:

y'+2xy=2

NiceSaid NiceSaid    2   15.03.2020 14:28    2

Ответы
avisotska avisotska  17.08.2020 19:23

Перепишем данное дифференциальное уравнение в виде:

\dfrac{y'}{y^3}+\dfrac{2x}{y^2}=2x^3

Введём замену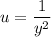 u=\dfrac{1}{y^2}, дифференцируя: 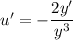u'=-\dfrac{2y'}{y^3}, получаем

u'-4ux=-4x^3

Умножим обе части уравнения на интегрирующий множитель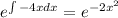 e^{\int -4x dx}=e^{-2x^2}

u'\cdot e^{-2x^2}+\Big(-4xe^{-2x^2}\Big)\cdot y=4x^3e^{-2x^2}\\ \\ \Big(u\cdot e^{-2x^2}\Big)'=-4x^3e^{-2x^2}\\ \\ \\ u\cdot e^{-2x^2}=\displaystyle -\int 4x^3e^{-2x^2}dx=[po~~ chastyam]=\dfrac{2x^2+1}{2}e^{-2x^2}+C\\ \\ \\ u=\dfrac{2x^2+1}{2}+Ce^{2x^2}

Выполним обратную замену

\dfrac{2x^2+1}{2}+Ce^{2x^2}=\dfrac{1}{y^2} — общий интеграл

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
raisa55555555 raisa55555555  01.10.2019 17:29
6. докажите, что значение выражения (3√3 + √13 ) (√13 - 3√3)является целым числом.​...
nastya19831507 nastya19831507  01.10.2019 17:29
Знайдіть координати 4 вершини паралелограма якщо а(2,6), в(4,7), с(8,10)...
Zepstro Zepstro  01.10.2019 18:20
Найти производную: 2-lnx/1+2arcsinx...
Taimy Taimy  01.10.2019 18:20
Система: {2(x+y)=22 {xy=28 помгите....
ighjkhh ighjkhh  01.10.2019 17:28
Построй график функции y=1−2x и по графику определи координаты точки пересечения графика функции с осью oy.1) заполни таблицу.2) используя таблицу, построй график функции и сравни...
фракталы фракталы  12.12.2020 02:31
Скажи миру 4. Площадь прямоугольного земельного участка равна (x ^ 2 -13x + 42) мл2. a) Если x2 -13x + 42 = (x + a) (x + b), тогда найдите значения a и b c) Если длина прямоугольника...
Noooo123456 Noooo123456  12.12.2020 02:31
1. ( ) Выберите функции, графики которых параллельны, ответ обоснуйте: y=0.2x+3 и y=15x+3 y=34x-5 и y=5x-7 y=4x+8 и y=4x-1 y=28x-11 и y=35x+9 ​...
F1RE000 F1RE000  12.12.2020 02:31
Напишите сокращенное квадратное уравнение с корнями x1 = -7 и x2 = 2, используя обратную теорему Виета...
katerina348 katerina348  12.12.2020 02:31
Выберите функции, графики которых параллельны, ответ обоснуйте: а) y=0,7x+ и y=7 в) y=2x-4 и y=-2x+4 б)y=-6x+2 и y=2-6x...
йврлгквы йврлгквы  12.12.2020 02:31
1)2x+2y З2х + y = 5Решение графическим...

Популярные вопросы