Решить дифференциальное уравнение с разделяющимися переменными: 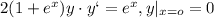
Другие вопросы по теме Алгебра
Популярные вопросы
- Якщо a-b=1,23,тоА) a=bБ) a bB) a bГ) a і b порівняти не можна...
2 - В таблице нужно ответить на вопросы...
1 - Все точки одной плоскости совпадают со всеми точками другой плоскости,...
1 - напишите сочинение письмо Правдина о беспорядках в доме госпожи Простаковой....
1 - Знайти значення виразу 5х-0,9 якщо х=(-2) умовляю ,мне сдавать тест через...
3 - Как изменяется внутренняя энергия стали при затвердевании,если ее масса...
3 - Общая характеристика и характеристика по отдельным признаки научного стиля...
3 - Ғабит Мүсіреповтың өмірбаяны туралы сұрақтар...
1 - 1. Сколько необходимо сжечь спирта, чтобы расплавить свинец массой 50 грамм...
1 - Сделайте вывод о роли пейзажа в повести Станционный смотритель...
3
дам решение диф.уравнения в общем виде
частное решение: при х=0; у(0)=0