Решить дифференциальное уравнение
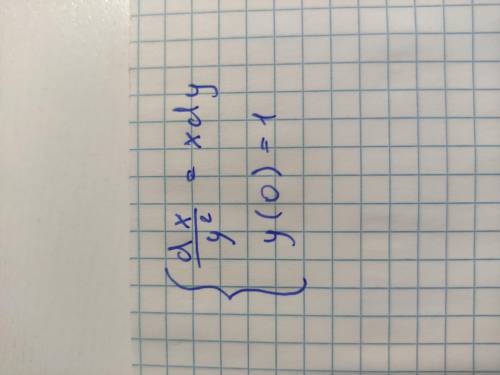
Другие вопросы по теме Алгебра
Популярные вопросы
- Крот ведет ночной образ жизни. какой это критерий?...
2 - ответе ! в чём кроется секрет обояние повести алые паруса а. грина?...
1 - Дополните предложения с правильной формой past continuous b: i (listen)...
3 - Местоположение название города в котором началось восстание под предводительством...
3 - X(3-x)=12-(4-x)² не сильна в уравнениях,...
3 - Сравните клиамт северной и южной америки.какие территорий материков...
1 - Что будет находиться в третьей строке после выполнения следующих действий?...
3 - Считается ли частица не частью сказуемого?...
3 - 20 словосочетаний с суффиксами ин и изн!...
3 - Какой выигрыш в силе должен был бы давать этот пресс при отсутствии...
2
Но ln0 не существует, поэтому задача Коши не имеет решения.
Если бы поменять значения "х" и "у" в начальных условиях, то