решить дифференциальное уравнение
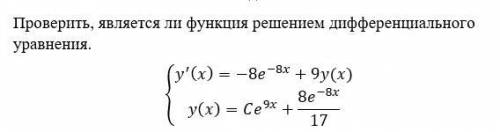
Другие вопросы по теме Алгебра
Популярные вопросы
- Історичний портрет короля сонце Всесв.Історія...
1 - СОР по химии Установи какие вещества образуются в результате горения металлов...
1 - Вариант 26. ВАПРОС ЛЁГКЫЙ ВАПРОС НА РИСУНКЕ БОЛЕЕ ПОДРОБНО...
3 - Вопрос Определите стихотворный размер. В ту ночь мы сошли друг от друга...
3 - Известно, что ΔCED — равнобедренный и ∢EDC=65°.Угол CED равен °....
3 - Определите ускорение свободного падения и первую космическую скорость на...
1 - решите не могу уже 3 часа сижу...
2 - 5.Изобразите координатной оси точки О(0);А(-7);С(3);В(4);К(-5).Определите...
1 - Письмовий твір-опис пам’ятки історії й культури на основі особистих вражень...
2 - Частинка що приєднує електрони в окисно-відновній реакції це...
1
Продифференцируем у(х)
Найденную производную подставим в первое уравнение системы:
Равенство выполняется
ответ: да, является