1. Алгебра
  2. Решить диф.ур. [tex]xy =4\sqrt{2x^2+y^2}+y[/tex]

Решить диф.ур.
xy'=4\sqrt{2x^2+y^2}+y

маринька маринька    3   29.12.2019 11:48    3

Ответы
кэтси кэтси  10.10.2020 23:39

данное дифференциальное уравнение является однородным.

Пусть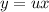 y=ux, тогда 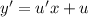y'=u'x+u, получаем

x(u'x+u)=4\sqrt{2x^2+u^2x^2}+ux\\ \\ x^2u'=4x\sqrt{2+u^2}\\ \\ x=0;~~~ u'x=4\sqrt{2+u^2}

Это диф. уравнение с разделяющимися переменными.

\displaystyle \int \dfrac{du}{\sqrt{2+u^2}}=\int \dfrac{4dx}{x}~~~\Rightarrow~~~~\ln\bigg|u+\sqrt{u^2+2}\bigg|=4\ln|x|+\ln C\\ \\ \\ u+\sqrt{u^2+2}=Cx^4

Выполнив обратную замену, получаем общий интеграл

\dfrac{y}{x}+\sqrt{\dfrac{y^2}{x^2}+2}=Cx^4

ПОКАЗАТЬ ОТВЕТЫ
lenaguceva lenaguceva  10.10.2020 23:39

ответ: во вложении Объяснение:


Решить диф.ур. <img src=" />
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
linalimeofficip01ef8 linalimeofficip01ef8  11.12.2020 20:15
полностью решить ​только правильно чтоб было...
kzifi kzifi  11.12.2020 20:15
Знайдіть градусну міру дуги, яка складає третину кола....
Andylov Andylov  11.12.2020 20:17
Кто решить с меня лайк + подписка Дано функцию f(x)=x^2-x-2 найдите значение х для которых f(x)=-4​...
Salahaddin001 Salahaddin001  11.12.2020 20:17
задание (фото прикреплено) я буду очень благодарна...
dimaloginkinozgu92 dimaloginkinozgu92  11.12.2020 20:18
Sinx -√2/2 решить с окружности...
Br0cHk1 Br0cHk1  11.12.2020 20:18
4∙(2х+5)=7х+13 С пояснением и...
Лисоооооооо Лисоооооооо  16.08.2019 15:10
Ничего не понимаю в корнях, если можно с подробным объяснением разложите на множители 6-9√2. варианты ответа: 1) 3√2(√2-√3) 2) √6(√2-3) 3) 3√2(√2-3) 4) 3√2(2-√3)...
laswsc11 laswsc11  16.08.2019 15:10
Разложить на множители: 3х+3у+бх+бу...
QueenAlinacom QueenAlinacom  16.08.2019 15:10
На прямой последовательно отмечены четыре точки а, б, с и d. при этом два отрезка ad и вс расположены так, что их середины . найдите длину отрезка bd, если ad =...
ShadowFlcus ShadowFlcus  16.08.2019 15:10
Решить уравнение. нужно. (2,5+3,2): 4,9 только 2,5 дробная и 4,9 тоже дробь....

Популярные вопросы