, решить данное неравенство.
Фото задания прикрепляется
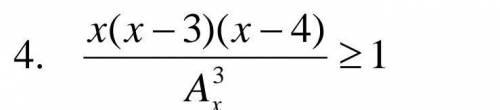
Другие вопросы по теме Алгебра
Популярные вопросы
- Лексическое значение слова жалобно а) скорбно. в) плаксиво. с)...
3 - Название заповедника, который создан на загрязненной территории...
2 - Решали в классе, почему тут такое чередование знаков - + - , ведь...
3 - Объёмкубакак из-менилсяобьём? г) модули про5. анализируя, заполните...
1 - 1.запишите 32-разрядное представление отрицательного вещественного...
1 - Небольшой рассказ на тему национальная библиотека беларуси...
1 - Укажите все звенья цепочки «ресурсы»-«факторы производства», если...
2 - Написать сочинение защита человеческой личности в произведении...
2 - Спишите, вставляя пропущенные буквы. выделите причастия, определите,...
1 - Составьте предложения, употребляя во части составных глагольных...
1
+ + + + + (0) - - - - - (1) + + + + + (2) - - - - - [2,5] + + + + +