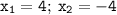Решить биквадратное уравнение:
x^4-12x^2-64=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Нужно поставить либо в present simplе или present continuous. 1)he (play) at the...
1 - Put the verbs in brackets into correct tense form. 1.our lass always (to do) some...
2 - Нужно поставить либо в present simplе или present continuous. you (enjoy) the film?...
3 - Сколькими можно расставить на полке 5 разных книг?...
3 - Складить будь ласка твир на тему ,, мий перший день в 5 класи...
2 - Взакрытом сосуде находится идеальный газ . на сколько % изменится давление , если...
1 - Найти смежные углы если их градусные меры относятся 5: 7...
1 - Найти смежный углы если их градусные меры относятся 5: 7...
1 - Плот проплыл потечению реки 24 кмза 8 часов, а моторных катер проплыл по течению...
2 - Запиши на языке: сумма цифр числа 287...
1
Пусть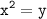 , тогда:
, тогда:
ответ: