1. Алгебра
  2. Решить b13. теплоход проходит

Решить b13. теплоход проходит по течению реки до пункта назначения 513км и после стоянки возвращается в пункт отправления.найдите скорость течения,если скорость теплохода в неподвижной воде равна 23км/ч,стоянка
длится8ч,а в пункт отправления теплоход возвращается через 54ч после отплытия из него.ответ дайте в км/ч.

звезда0ютуба звезда0ютуба    1   10.03.2019 05:50    1

Ответы
Глебочек Глебочек  06.06.2020 23:40

Пусть х - скорость течения реки. Тогда скорость теплохода по течению составляет 23+х км/ч, против течения - 23-х км/ч. Теплоход проходит расстояние от пункта отправления до пункта назначения за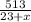 \frac{513}{23+x} часов, а обратно за - 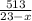\frac{513}{23-x} часов. Составим уравнение

\frac{513}{23+x}+\frac{513}{23-x}+8=54 

\frac{513}{23+x}+\frac{513}{23-x}+8-54=0

\frac{513}{23+x}+\frac{513}{23-x}-46=0

Приведем к общему знаменателю

\frac{513(23-x)}{(23+x)(23-x)}+\frac{513(23+x)}{(23-x)(23+x)}-\frac{46(23-x)(23+x)}{(23-x)(23+x)}=0 

\frac{11799-513x}{(23+x)(23-x)}+\frac{11799+513x}{(23-x)(23+x)}-\frac{46(529-x^{2})}{(23-x)(23+x)}=0 

\frac{11799+11799-23x+23x}{(23+x)(23-x)}-\frac{24334-46x^{2}}{(23-x)(23+x)}=0 

\frac{23598-24334+46x^{2}}{(23+x)(23-x)}=0 

\frac{-736+46x^{2}}{(23+x)(23-x)}=0 

Найдем корни уравнения при условии, что  

(23+x)(23-x)\neq0 

23+x\neq0                     23-x\neq0 

x\neq-23                       x\neq23 

Тогда

-736+46x^{2}=0 

46x^{2}=736 

x^{2}=16 

x=\sqrt{16} 

x_{1}=-4 - не удовлетворяет условию

x_{2}=4  

ответ: скорость течения реки составляет 4 км/ч

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ladysachenko20 ladysachenko20  15.12.2021 08:54
Решить систему и построить график функции y =x² y =4...
xag xag  15.12.2021 08:54
Упроститеа) 3√2+3√8-√98б) (3√2)+ (2√48)в) 2-√...
tanuskin798 tanuskin798  15.12.2021 08:54
Упроститеа) 3√2+3√8-√98б) (3√2)+ (2√48)в) (2-√3)²...
karinochka666 karinochka666  15.12.2021 08:53
Полный ход решение показывайте чтоб понятно было...
pep4 pep4  15.12.2021 08:53
9. Решите графически уравнение: а) х^2 – 6х + 5 = 0 б) 3x + 9 +x^2 = 0...
tarasbulba204 tarasbulba204  26.06.2019 14:00
Найдите производную функции f(х) =(х^5 -4\x)^11 f(x) = 1\ 2x+√x f(x) =(x-√x)^4 - √x\ x+3 -24\(3-4x^3)^5...
Brokenheart94 Brokenheart94  26.06.2019 14:00
Кграфику функции y=x^2-2+3 проведены касательные в точках (0; 3) и (2; 3).найти координаты точки пересечения этих касательных....
KaterinaFadeeva KaterinaFadeeva  26.06.2019 14:00
Разложите многочлен на множители. 9x^2-10a^3 +6ax-15ax^2 я сгруппировала 1 с 3 и 2 с 4 получилось (3x-5a^2)(3x+2a) проверьте ....
Dim102 Dim102  26.06.2019 14:00
Бассейн наполняется через две трубы за 6 часов, если открыть только одну трубу, то бассейн наполнится за 7 часов. за какое время можна наполнить бассейн, если открыть...
nastikus555 nastikus555  26.06.2019 14:00
Разложите на множители b)m^2(n+1)+2m(n+1) г) a(a--1)...

Популярные вопросы