РЕШИТЬ 2 ЗАДАЧИ: 1. Периметр прямоугольника равен 360 м, а
его площадь 7700 м2. Найдите длины сторон
прямоугольника.
3. Один из корней уравнения х2 - 26х + q = 0
равен 14 Найдите другой корень и свободный
член q.
Другие вопросы по теме Алгебра
Популярные вопросы
- Как отзывались о Мандельштаме жители Дома искусств?...
2 - Эссе Хан Жангир- народный батыр...
1 - Придумать задачу про банк ( используя вклад, займы, проценты) для...
2 - Английский 8 класс контрольная помагите...
1 - K2SO4+H2SO4=? уравнения реакции...
3 - Реши Систему Линейных Уравнений...
2 - Не большое сочинение на тему Мхи минимум 10 предложений)...
1 - Найди значение выражения: (13,9−14,4):0,4 (ответ округли до десятых)....
3 - Разбирите предложение: Пускай мама купит мне яблоки. (двухсоставное...
1 - А) Представь, что ты тоже учился в этом классе. Расскажи этусооно...
1
Объяснение:
1) Р = (а + b)*2 = 360
S = a * b = 7700
3)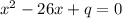 , x1 = 14, q = ?
, x1 = 14, q = ?
q = 168
x² + px + q = 0 сумма корней равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:
x₁ + x₂= -p
x₁ · x₂= q
14 + x₂ = 26
x₂=26-14=12
q=14*12=168
x²-26x+168=0 - при желании можно проверить, подставив в уравнение корни, можно для проверки решить через дискриминант.
144-312+168=0
задача
70 м; 110 м
Периметр прямоугольника со сторонами а и b: Р = 2 * (a + b).
Площадь прямоугольника: S = a * b.
Следовательно, получим систему уравнений:
2 * (a + b) = 360.
a * b = 7700.
Решаешь системой уравнений
(a + b) =230
a=7700/b
7700/b+b=230
b^2 – 230 * b + 7700=0