1. Алгебра
  2. решить: 2+tg^2 x, если

решить: 2+tg^2 x, если cos =0.5

emir07 emir07    1   16.07.2021 02:01    4

Ответы
aculkow2017 aculkow2017  16.07.2021 06:00

Объяснение:

tg²x=sin²x/cos²x= 2sinxcosx/cos²x-sin²x= 2(√1-cos²x)cosx/cos²x×(1-cosx)= 2√1-1/4)×1/2/1/4×(1-1/2)= 2√3/4 ×1/2/:1/4(1-1/2)=√3/2/1/8= 4√3

ПОКАЗАТЬ ОТВЕТЫ
LadnoOK LadnoOK  16.07.2021 06:00

5

Объяснение:

Тригонометрическая единица:

\sin^2x+\cos^2x=1

Разделим обе части на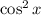 \cos^2x (по условию он не равен нулю):

\frac{\sin^2x}{\cos^2x} +\frac{\cos^2x}{\cos^2x} =\frac{1}{\cos^2x}\\(\frac{\sin x}{\cos x})^2 +1=\frac{1}{\cos^2x}\\\rm tg^2x+1=\frac{1}{\cos^2x}

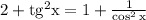
Отсюда 2+\rm tg^2x=1+\frac{1}{\cos^2x}

Имеем:

2+\rm tg^2x=1+\frac{1}{0.5^2}=1+\frac{1}{\frac{1}{4} }=1+4=5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
mar244144 mar244144  02.09.2019 20:10
Найдите область определения функции у=корень из 2х^2-5x-3...
neli2017 neli2017  02.09.2019 20:10
Решить уравнение: (x+1)^4+(x+1)^2-6=0...
Zeka211 Zeka211  02.09.2019 20:10
(x+1)^4 +(x+1)^2-6=0 решите уравнение...
Георгий07 Георгий07  02.09.2019 18:33
Сподробностями над каждым ! ! 5- (7/9 -1/6) : 2,5...
Ivan700076 Ivan700076  02.09.2019 20:10
Постройте график функций y=-x+6 с графика найдите а) наибольшее или наименьшее значение на отрезке [1; 2] б) значение переменной x, при которых y=0; y= 0...
Алла36 Алла36  02.09.2019 18:40
Найти производную функции y=4x-sin2x+4 корень из2 cosx[tex](cosx) = - sinx[/tex]​...
Вандализм Вандализм  11.12.2019 19:15
Найдите произведение многочлена и одночлена...
innaalekseenko1 innaalekseenko1  11.12.2019 19:15
2/3 корень 21 ,3 корень 5, и 7 расположите числа в порядке возрастания...
puremoorning puremoorning  11.12.2019 19:14
((а^1/3-а^7/3)/(а^1/3-а^4/3))- ((а^-1/3-а^5/3)/(а^2/3+а^-1/3))...
alexandrapavlov1 alexandrapavlov1  11.12.2019 20:32
На рисунке 10.8 угол amk=acb, ak=mk. докажите, что треугольник abc равнобедренный. ​...

Популярные вопросы