Решить!
1)4 - 4x2 =0
2)16x2 + 22x = 38
3)x2 = 30 + x
4)16 - 8x + x2 =0
5)5x2 - 26x + 5 =0
Другие вопросы по теме Алгебра
Популярные вопросы
- Сочинение на тему моё любимое произведение за курс 7 класса В прекрасном и яростном...
1 - ВПР. Обществознание. 6 класс. Вариант 2 КОДПривлекая обществоведческие знания,...
2 - Определите количество последовательностей из нулей и единиц длины N (длина —...
3 - Две прямые касаются окружности с центром о в точках а и в и пересекаются в точке...
1 - Создать электронную книгу (тема на ваше усмотрение) В проекте должно быть1....
1 - Выразите: a) В граммах: 2 кг 350 г; 1 кг 60 г; b) в килограммах: 2 т 725 кг;...
3 - Две прямые касаются окружности с центром о в точках а и в и пересекаются в точке...
3 - Составьте рассказ на основе услышанного, что вам запомнилось больше всего? Почему?...
3 - с геометрией нужно сделать задания 2,3,12,20: задания на скриншотах...
1 - Who you think the people are. what you think the problem ishow they are feeling...
1
1) ± 1
2) 1;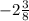
3) 6; - 5
4) 4
5) 5; 0, 2
Объяснение:
1) 4 - 4х² = 0
- 4х² = - 4
4х² = 4
х² = 1
х = ± 1
2) 16х² + 22х = 38
16х² + 22х - 38 = 0
8х² + 11х - 19 = 0
D = b² - 4ac = 121 + 608 = 729 = 27² ⇒ 2 корня:
3) х² = 30 + х
х² - х - 30 = 0
D = b² - 4ac = 1 + 120 = 121 = 11² ⇒ 2 корня:
4) 16 - 8х + х² = 0
х² - 8х + 16 = 0
D = b² - 4ac = 64 - 64 = 0 ⇒ 1 корень:
5) 5x² - 26x + 5 = 0