Реши уравнение с натуральными значениями букв: a! +b! +c! =d!
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите биквадратное уравнение x⁴-4x²+4=0...
1 - Решите систему уравнений графическим x+y=72x-y=-1...
1 - Задание 1.Выберите основные причины и предпосылки национально- освободительного...
1 - 3.Потери кислорода в воздухе восполняют … А) промышленные предприятия B) растения...
3 - УМОЛЯЮ изобразите треугольник полученный из треугольника АВС параллельным переносом...
3 - Задание 8. От глаголов собрать раздать, продать, применитьобразуйте деепричастия:1....
1 - 2. ответьте на вопрос: Какие можно выделить общие сходства в развитие государств?...
1 - Абайдың бірінші қара сөзінде қандай кейіпкер бейнесі бар?Лирикалық кейіпкерРомантикалық...
1 - Число, 1,(5) часть которого равна 25...
2 - Горение топлива и выделение энергии Выбери пути решения проблемы парникового...
2
1-й случай.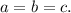 Разделив уравнение на
Разделив уравнение на 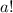 , получаем
, получаем 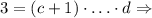 в правой части на самом деле один множитель;
в правой части на самом деле один множитель; 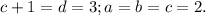 Проверка:
Проверка: 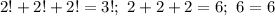 - верно. Итак, одно решение найдено.
- верно. Итак, одно решение найдено.
2-й случай.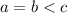 . Разделив уравнение на
. Разделив уравнение на 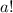 , получаем
, получаем 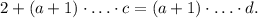 Следовательно,
Следовательно, 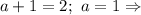 уравнение имеет вид
уравнение имеет вид 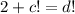 Но два факториала не могут отличаться на 2, поэтому в этом случае уравнение решений не имеет.
Но два факториала не могут отличаться на 2, поэтому в этом случае уравнение решений не имеет.
3-й случай.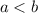 . Разделив уравнение на
. Разделив уравнение на 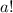 , получаем
, получаем 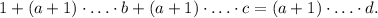 Такое уравнение не может иметь решений, так как все слагаемые, кроме первого, делятся на a+1.
Такое уравнение не может иметь решений, так как все слагаемые, кроме первого, делятся на a+1.
ответ: a=b=c=2; d=3