Решение необязательно, но приветствуется. Спам = жалоба. Примечание: этот тест дали мне не как тест, а просто как задания, так что я могу отправить их сюда.
Другие вопросы по теме Алгебра
Популярные вопросы
- с тестом. 11 класс, Алгебра. Исследование функций с производной...
1 - 1 6. Лыжник проходит за час 11 1/5км. Сколько километров он пройдет заполчаса,...
1 - .Білім-ғылымға шақыратын басқа ақынның өлеңімен салыстыру («Венн диаграммасы»:...
2 - Выделите особенности растений и животных: Растения (по высоте) Поскольку в Пустыне...
1 - Що об єму ж мужа забрати або синові або дітям брат якщо ніхто не буде нести...
1 - Найдите число корней уравнения 1+sinx=ctgx+cosx на промедутке (3пи;пи) С решением!...
2 - Перечислите как наука повличла на развития хозяйства в древнем египте...
3 - Задания 1. Приведи в соответствие с Традиционные обрядовые песни1. Колыбельные2....
2 - У человека близорукость (А) доминирует над нормальным зрением, а нормальный...
1 - нужнозадание: используйте словосочетания в таблице....
2
а)
б)
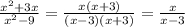
2.а)
б)
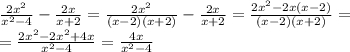
3.