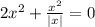 Решение через дискриминант
Решение через дискриминант
Другие вопросы по теме Алгебра
Популярные вопросы
- Органы выделения у аскариды и у дождевого червя...
2 - Дайте полное описание химического элемента по названию и количеству...
2 - Чем меньше порядковый номер вышеперечисленных элементов,тем сильнее...
1 - Придумать сказку про ёлку своими словами 1-2 листа НУЖНО Помагитеее...
2 - Определи какой план подойдёт к данному тексту 1 или 2...
1 - Найдите координаты точек симметричных точке А(-3;1) относительно:...
3 - Вычислите 7/10-(3/4-3/5)+7/8 с решением) У меня сор...
3 - Соедини исходящие из ленты времени в какой последовательности жили...
3 - Исторический портрет 1 подсказка.• Он был человеком высокогороста,...
1 - Во что превратился бы земной шар без солнечной системы ? Заранее...
1
x = 0 не удовлетворяет ОДЗ
-1/2 не подходит условию x ≥ 0
1/2 не подходит условию x < 0
ответ: нет корней