решение целого уравнения. 1) 10x^3 - 20x^2 - x + 2 = 0

2) x^4 - 3x^2 - 4 = 0

Question

Алгебра: решение целого уравнения. 1) 10x^3 - 20x^2 - x + 2 = 02) x^4 - 3x^2 - 4 = 0

гога61 · Answer

Задание: решить уравнения.Объяснение:ОтсюдаПусть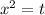 , тогда При t=-1 уравнение x²=t действительных решений не имеет.При t=4: x²=4, x=±2....

решение целого уравнения. 1) 10x^3 - 20x^2 - x + 2 = 02) x^4 - 3x^2 - 4 = 0