РЕБЯТА С МАТЕШОЙ а то не аттестация будет(
Ничо не понятно
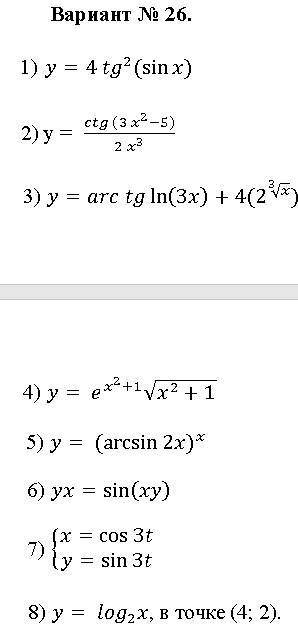

Другие вопросы по теме Алгебра
Популярные вопросы
- Задание 5 выбрать однин ответ...
2 - Позначте рядок, у якому всі прислвники записані правильноА по сусідськи,...
1 - Яку частку від загальної кількості населення України складають чоловіки та...
1 - 1.Сума коефіцієнтів у рівняння реакції 1.Ba+H2O=Ba(OH)2+H2 2.N2O5+H2O=HNO3...
3 - Переместите в соответствующий прямоугольник значение угла поворота, при котором...
2 - Ребята,я кнш понимаю тут только в знаниях,короче как поставить фото сюда...
2 - На уроке английского трое ребят (Хлебников, Рыбаков и Ткачёв) выступали перед...
2 - Какой вид прилагательного осеннее небо...
1 - Мне нужен сжатый перессказ робин гуда...
3 - Що являє собою ,,Червона книга ? Які види реєструються ,,Червоною книгою...
1
по формуле:
формула: