Ребят решить, кто решит правильно очень нужно! найдите наименьшее значение выражения
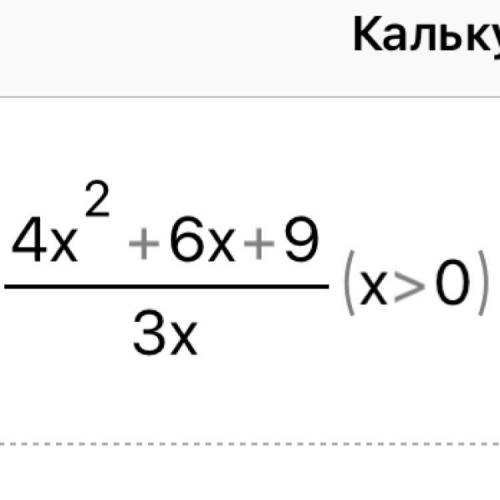
Другие вопросы по теме Алгебра
Популярные вопросы
- Высота, проведенная к основанию равнобедренного треугольника, равна...
2 - Втреугольнике abc известно , что угол с=90 градусов .найдите : 1)bc,если...
3 - Составьте график, демонстрирующий динамику развития промышленности...
1 - Женское имя, в котором есть 30 займеников я?...
2 - Что такое хорошо и что такое плохо.о чём просит автор? как называют...
2 - Іть будь ласка обчислити масову частку оксигену у глюкозі...
1 - What was the doctors decision about his patients health? ниже текст...
3 - 1% процент книги которую читал сережа состовляет 4 страницы сколько...
2 - Сколько натуральных чисел от 1 до 1000 включительно, которые не делятся...
3 - На кинофестиваль 42 художественных и 28 документальных фильмов. каждый...
1
6
Объяснение:
Тут еще надо доказать, что это минимум. Но можно рассуждениями.
При x=0 функция неограниченно большая, а при x=1 поменьше, следовательно функция убывает и это минимум.
f(x) = (4x^2 + 6x + 9) / (3x)
возьмем производную :
f'(x) = ((4x^2 + 6x + 9)' * 3x - (4x^2 + 6x + 9) * (3x)')/ (3x)^2 = ((8x + 6) * 3x - (4x^2 + 6x + 9) * 3) / (9x^2) = (24x^2 + 18x - 12x^2 - 18x - 27)/(9x^2) = (12x^2 - 27)/(9x^2)
Приравняем производную к нулю и получим точки экстремума:
(12x^2 - 27)/(9x^2) = 0
12x^2 - 27 = 0
x^2 = 27/12
x = +- sqrt(27/12)
По правилу Дарбу на промежутке
(- бесконечность ; - sqrt(27/12)) функция возрастает
( - sqrt(27/12) ; 0 ) возрастает
(0 ; sqrt(27/12) ) убывает
(sqrt(27/12) ; + бесконечность) возрастает
значит точка sqrt(27/12) - точка минимума
подставим ее в уравнение и получим результат равный 6
ответ: 6