Разве в функции 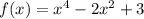на отрезке [-4; 3] наибольшее значение функции не равно 227? Просто в другом вопросе эксперт написал наибольшее значение как 3

227

Объяснение:

f(x)=x⁴-2x²+3

находим производную:

f'=(х⁴-2x²+3)'=4х³-2*2х+0= 4х³-4х

приравниваем производные к 0:

f' = 4x³-4x=0

находим критические точки:

4x³-4x=0

4х(х²-1)=0

4х(х-1)(х+1)=0

х=0 или х-1=0 или х+1=0

х1=0, х2=1, х3=-1

смотри прикрепленное изображение 1

необходимо найти наибольшее значение на промежутке [-4;3] (прикрепленное изображение 2)

Для нахождения наибольшего значения функции на заданном отрезке достаточно вычислить её значения на концах отрезка ( х=-4 и х=3 ) и в точке максимума (х=0).

f(x)=x⁴-2x²+3 →

Эти значения функции:

f(-4)=(-4)⁴-2*(-4)²+3=256-32+3=227

f(0)=0⁴-2*(0)²+3=0-0+3=3

f(3)=(3)⁴-2*(3)²+3=81-18+3=66 →

Наибольшее значение функции в точке х=-4 и f(x)=227