1. Алгебра
  2. разобраться с логарифмическими

разобраться с логарифмическими уравнениями. Номер 829 и 839

roky210 roky210    2   30.04.2020 00:31    2

Ответы
79854246143TATIANA 79854246143TATIANA  14.10.2020 03:51

№822

log_{x+1}(x-\frac{1}{2}) = log_{x-\frac{1}{2}}(x+1)\\log_{x+1}(x-\frac{1}{2}) = \frac{1}{log_{x+1}(x-\frac{1}{2})}\\log_{x+1}^2(x-\frac{1}{2}) = 1\\log_{x+1}(x-\frac{1}{2}) = 1 = x+1 = x - \frac{1}{2} = x \in \varnothing\\ log_{x+1}(x-\frac{1}{2}) = -1 = (x+1)^{-1} = x-\frac{1}{2} = \frac{1}{x+1} = x-\frac{1}{2} = (x+1)(x-\frac{1}{2} )=1 = x^2 + \frac{1}{2}x - \frac{3}{2} = 0\\ D = \frac{1}{4} + 6 = \frac{25}{4} = (\frac{5}{2})^2\\

x_1_2=\frac{-\frac{1}{2}\pm\frac{5}{2}}{2} = 1, -\frac{3}{2}

Отрицательный корень не подходит по ОДЗ. Остается только x = 1

ответ: x = 1

№825

(1.25)^{1-log_2^2x} = (0.64)^{2log_22x}\\(\frac{5}{4})^{1-log_2^2x} = ((\frac{5}{4})^{-2})^{2log_22x}\\(\frac{5}{4})^{1-log_2^2x} = (\frac{5}{4})^{-4log_22x}\\1-log^2_2x = - 4log_2(2x)\\1-log^2_2x = -4(log_22 + log_2x)\\1-log^2_2x = -4 - 4log_2x\\log^2_2x-4log_2x-5=0\\\frac{D}{4} = 4 + 5 = 3^2\\ log_2x = 2 \pm3 = -1, 5\\1) log_2x = -1 = x = \frac{1}{2}\\ 2) log_2x = 5 = x = 2^5 = 32\\

По ОДЗ все походит, можно писать ответ

ответ: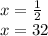 x = \frac{1}{2}\\x = 32

№826

x^{lgx} = 1000x^2\\lg(x^{lgx}) = lg(1000x^2)\\lgx*lgx=lg1000+lgx^2\\lg^2x=3+2lgx\\lg^2x-2lgx-3=0\\lg^2x-2lgx+1-4=0\\(lgx-1)^2-2^2=0\\(lgx-1-2)(lgx-1+2)=0\\(lgx-3)(lgx+1)=0\\lgx = 3 = x = 1000\\lgx = -1 = x = \frac{1}{10}\\

По ОДЗ все ок, можно писать ответ.

ответ: x = \frac{1}{10}\\ x = 1000

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Ivan190901 Ivan190901  03.07.2019 01:10
Решите уравнение 7 (а-6)=3 (6-а)- 20...
striyskiy1 striyskiy1  03.07.2019 01:10
Нужно ! сократите дроби. 1)3x/2ax 2)12xy/20y 3)24m^3n/16m^2n^2 4)xy^3z^5/x^5y^3z 5)3x+3y/3x-3y 6)2ab-2c/2ac-2b 7)a^2b+ab/abc 8)a^2b+ab/ab 9)3xy/3x^2y-6xy 10)2mnp/2m^2p-6mp...
anton20063 anton20063  03.07.2019 01:10
Раскройте скобки -0,4(-5+1,5y); (х+3,+4,5) и 1,4(а--2а)...
Ыыыап Ыыыап  03.07.2019 01:10
4.2*0.016 0.15*0.8*0.75 0.4*2.8 12.5*0.36...
Kylie15 Kylie15  06.10.2019 21:54
15 ответьте на кауие сможете желательно все​...
кари345 кари345  06.10.2019 21:50
(много )1. решите уравнение: a) x^3-x^2-19x-17=0 б) x^3+3x^2-3x-14=02. решите уравнение, используя введение новой переменной: (x+3)(x+4)(x+5)(x+6)=16803. решите симметрическое...
Lovedashuta Lovedashuta  06.10.2019 21:50
Решите примеры: 1)(x-1)(x+5) =0 2)x+[tex]\sqrt{x+1}[/tex]=1 3)[tex]\frac{2}{x}[/tex]+2=[tex]\sqrt{4+\frac{1}{x}\sqrt{64+\frac{144}{x^{2} } } }[/tex]...
ЛизаМэй ЛизаМэй  06.10.2019 23:10
Дано, что be — биссектриса угла abc. ba⊥daиec⊥cb. вычислиcb, если da=9 см, ba=12 см, ec=6,3 см. сначала докажем подобие треугольников. в каждое окошечко пиши одну...
Королева1986 Королева1986  06.10.2019 23:10
Какое слово является деепричастием дорогая подорожал в подорожала дорожавший...
egorivanov2000 egorivanov2000  06.10.2019 21:47
Свообще не знаю, как решать подобного типа. уравнение то я решу, а как на вопрос ответить?...

Популярные вопросы