РАЗОБРАТЬСЯ
ответ:
(-1; 0)U[1; бескон.)
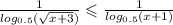
Другие вопросы по теме Алгебра
Популярные вопросы
- Какое утверждение соответствует содержанию текста ?...
1 - Су мен бор кесегін қалай бөдуге болады...
2 - Во сколько раз нужно увеличить исходную концентрацию веществ чтобы скорость...
1 - Напишите уравнение электролиза: а) расплава CuCl2; б) раствора КCl;...
3 - Було 100 яшчиків І забрали 60 яшчиків Скільки залишилося яшчиків...
3 - Преобразуйте следующие единицы измерение...
3 - Колесо едущей машины за 54 сделало 300 оборотов . длина колеса 1м 8см.найдите...
2 - Мәтіннен біріккен сөздерді тауып жаз Оқжетпес туралы аңыз...
3 - В ромбе ABCD угол ACD = 26градусов, найдите все углы...
1 - 3-тапсырма. Екпін түрлерін қолдана отырып, мәтінді оқы. Негізгі және қосымша...
2
ответ во вложении
ответ: ∈(-1;0)∪[1;+∞)
∈(-1;0)∪[1;+∞)
Объяснение:
ОДЗ: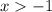 →
→ 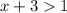 , поскольку основание логарифма
, поскольку основание логарифма  , то левая часть всегда отрицательна.
, то левая часть всегда отрицательна.
Рассмотрим сначала случай, когда правая часть неравенства положительна, то есть основание логарифма меньше единицы: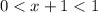 , в этом случае неравенство выполняется.
, в этом случае неравенство выполняется.
Теперь рассмотрим основной случай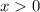 , в этом случае правая часть отрицательна, поэтому, учитывая, что
, в этом случае правая часть отрицательна, поэтому, учитывая, что  неравенство равносильно:
неравенство равносильно:
Поскольку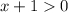 можно возвести в квадрат
можно возвести в квадрат
Объединяя случаи имеем: