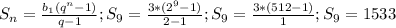Разность между четвертым и вторым членами прогрессии равна 18, а между пятым и третьим членами равна 36. найти сумму первых девяти членов.
Другие вопросы по теме Алгебра
Популярные вопросы
- Объясни почему с табличного случая деления 42разделить7=6...
1 - Поставь ударение в словарных словах.подчеркни безударную главную. библиотека...
1 - Фонетический разбор слова сабын на казахском языке...
3 - Впараллелограмме abcd ac=15см середина m стороны ab соединена отрезком с...
3 - Выписать пары однокоренных слов и выделить в них корень гора - горный, лиса...
2 - 5450кг и 5т 4ц 50кг будет ли это равенства...
1 - Построить график функции y=x^-4 поделить на x...
2 - На лугу пас лось несколько коров...
3 - Вкаком глаголе допущена ошибка: неверно выделена буква, обозначающая ударный...
2 - Сочинение как вы думаете почему египтяне так уважительно относились к реке...
3
По условию задачи:
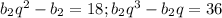
b4-b2=18; b5-b3=36.
Выразим всё через b2:
Получилась система уравнений: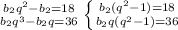
Разделим второе на первое, получим: q=2 подставим в первое уравнение: b2*4-b2=18; 3b2=18; b2=6.Найдём b1:b2=b1q; 6=b1*2; b1=3
Найдём сумму первых девяти членов по формуле: