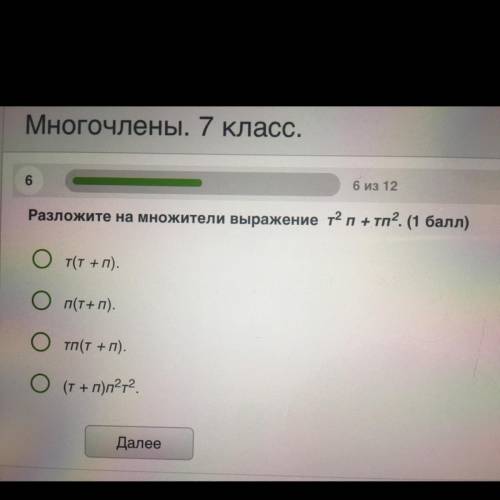
Разложите на множители выражение т2п+тп2.

тп(т+п)  

Объяснение:

т²п+тп²

тп(т+п)  

Более подробно:

т²п+тп²

многочлен можно представить как ттп+тпп или тп*т+тп*п. Так как у обоих есть тп его можно вынести за скобку тп(т+п).

Вынесение общего множителя за скобки проводится в суммах, в которых каждое из составляющих из слагаемых представляет собой произведение, причем в каждом из этих произведений присутствует одинаковый множитель. Этот одинаковый множитель и называется общим множителем, и именно он выносится за скобки. Например: ab+ac=a(b+c)

Разложить многочлен на множители означает представить его в виде произведения двух или нескольких многочленов.

Многочлен это алгебраическое выражение, представляющее сумму или разность нескольких одночленов. Например: ax²+bx-c, a+c, a-b.

Одночлен это алгебраическое выражение, представляющее собой произведение величин, в к-ром отдельные элементы не разъединены знаками плюс или минус. Например: ab, a, 2c, 10b.

Объяснение:

Разложить многочлен на множители означает представить его в виде произведения двух или нескольких многочленов.

т²п+тп²=ттп+тпп=тп*т+тп*п=тп(т+п)